Coupled Oscillator: Hellie: Difference between revisions
Jump to navigation
Jump to search
New page: ===Problem Statement=== |
|||
| (18 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
===Problem Statement=== | ===Problem Statement=== | ||
'''Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes of the system. Solve Using the Matrix Exponential''' | |||
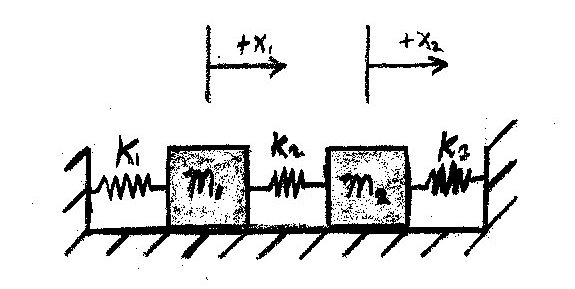
[[Image:Coupled_Oscillator.jpg]] | |||
'''Initial Conditions:''' | |||
:<math>m_1= 10 kg\,</math> | |||
:<math>m_2 = 10 kg\,</math> | |||
:<math>k1=100 N/m\,</math> | |||
:<math>k2=150 N/m\,</math> | |||
:<math>k3=100 N/m\,</math> | |||
'''F=ma''' | |||
:<math>\ddot{x_1}=\frac{x_1(k_1-k_2)}{m_1}-\frac{x_2*k_1}{m_1}\,</math> | |||
:<math>\ddot{x_2}=\frac{x_2(k_1+k_2)}{m_2}-\frac{x_1*k_1}{m_2}\,</math> | |||
'''State Equations''' | |||
<math> | |||
\begin{bmatrix} | |||
\dot{x_1} \\ | |||
\ddot{x_1} \\ | |||
\dot{x_2} \\ | |||
\ddot{x_2} | |||
\end{bmatrix}\, | |||
</math> | |||
= | |||
<math> | |||
\begin{bmatrix} | |||
0&1&0&0 \\ | |||
\frac{(k_1-k_2)}{m_1}&0&\frac{-k_1}{m_1}&0 \\ | |||
0&0&0&1 \\ | |||
\frac{-k_1}{m_2}&0&\frac{(k_1+k_2)}{m_2}&0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
x_1 \\ | |||
\dot{x}_1 \\ | |||
x_2 \\ | |||
\dot{x}_2 | |||
\end{bmatrix} | |||
+ | |||
\begin{bmatrix} | |||
0&0&0&0 \\ | |||
0&0&0&0 \\ | |||
0&0&0&0 \\ | |||
0&0&0&0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
0\\ | |||
0\\ | |||
0\\ | |||
0 | |||
\end{bmatrix} | |||
</math> | |||
'''With the numbers...''' | |||
<math> | |||
\begin{bmatrix} | |||
\dot{x_1} \\ | |||
\ddot{x_1} \\ | |||
\dot{x_2} \\ | |||
\ddot{x_2} | |||
\end{bmatrix}\, | |||
</math> | |||
= | |||
<math> | |||
\begin{bmatrix} | |||
0&1&0&0 \\ | |||
\frac{(-50 N/m)}{10 kg}&0&\frac{-100 N/m}{10 kg}&0 \\ | |||
0&0&0&1 \\ | |||
\frac{-100 N/m}{10 kg}&0&\frac{(250 N/m)}{10 kg}&0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
x_1 \\ | |||
\dot{x}_1 \\ | |||
x_2 \\ | |||
\dot{x}_2 | |||
\end{bmatrix} | |||
</math> | |||
<math> | |||
\begin{bmatrix} | |||
\dot{x_1} \\ | |||
\ddot{x_1} \\ | |||
\dot{x_2} \\ | |||
\ddot{x_2} | |||
\end{bmatrix}\, | |||
</math> | |||
= | |||
<math> | |||
\begin{bmatrix} | |||
0&1&0&0 \\ | |||
-5&0&-10&0 \\ | |||
0&0&0&1 \\ | |||
-10&0&25&0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
x_1 \\ | |||
\dot{x}_1 \\ | |||
x_2 \\ | |||
\dot{x}_2 | |||
\end{bmatrix} | |||
</math> | |||
'''Eigenvalues''' | |||
:<math>\lambda_1=-5.29412\,</math> | |||
:<math>\lambda_2=2.83333i\,</math> | |||
:<math>\lambda_3= -2.83333i\,</math> | |||
:<math>\lambda_4=0\,</math> | |||
'''Eigenvectors''' | |||
:<math>k_1=\begin{bmatrix} | |||
-.05379\\ | |||
.28475 \\ | |||
.17764 \\ | |||
-.94046 | |||
\end{bmatrix}</math> | |||
:<math>k_2=\begin{bmatrix} | |||
-.31854i\\ | |||
.90253 \\ | |||
-.09645i\\ | |||
.27326 | |||
\end{bmatrix}</math> | |||
:<math>k_3=\begin{bmatrix} | |||
.31854i\\ | |||
.90253 \\ | |||
.09645i \\ | |||
.27326 | |||
\end{bmatrix}</math> | |||
:<math>k_4=\begin{bmatrix} | |||
-.05379\\ | |||
-.28475 \\ | |||
.17764 \\ | |||
.94046 | |||
\end{bmatrix}</math> | |||
'''Standard Equation''' | |||
:<math>x=c_1k_1e^{\lambda_1 t}+c_2k_2e^{\lambda_2 t}+c_3k_3e^{\lambda_3 t}+c_4k_4e^{\lambda_4 t}</math> | |||
:<math>\ x=c_1</math><math>\begin{bmatrix} | |||
-.05379\\ | |||
.28475 \\ | |||
.17764 \\ | |||
-.94046 | |||
\end{bmatrix}\,</math><math>e^{-5.29412}+ c_2\,</math><math> | |||
\begin{bmatrix} | |||
-.31854i\\ | |||
.90253 \\ | |||
-.09645i\\ | |||
.27326 | |||
\end{bmatrix}\,</math><math>e^{2.83333i}+ c_3\,</math><math>\begin{bmatrix} | |||
.31854i\\ | |||
.90253 \\ | |||
.09645i \\ | |||
.27326 | |||
\end{bmatrix}\,</math><math>e^{-2.83333i}+ c_4\,</math><math>\begin{bmatrix} | |||
-.05379\\ | |||
-.28475 \\ | |||
.17764 \\ | |||
.94046 | |||
\end{bmatrix}\, | |||
</math><math>e^{0}\,</math> | |||
'''Eigenmodes''' | |||
:There are two eigenmodes for the system | |||
::1) m1 and m2 oscillating together | |||
::2) m1 and m2 oscillating at exactly a half period difference | |||
'''Matrix Exponential using transformation z=Tx''' | |||
<math>T^{-1}=[k_1|k_2|k_3|k_4]\,</math> | |||
<math>z=Tx\,</math> | |||
<math>\dot{z}=TAT^{-1}z \,</math> | |||
<math>\dot{z}=\,</math> | |||
<math>\begin{bmatrix} | |||
-5.2941&0&0&0 \\ | |||
0&2.833i&0&0 \\ | |||
0&0&-2.83333i&0 \\ | |||
0&0&0&5.2941 | |||
\end{bmatrix}\, | |||
</math> | |||
<math>z\,</math> | |||
<math>B=TAT^{-1}=\begin{bmatrix} | |||
-5.2941&0&0&0 \\ | |||
0&2.833i&0&0 \\ | |||
0&0&-2.83333i&0 \\ | |||
0&0&0&5.2941 | |||
\end{bmatrix}\,</math> | |||
<math>z=e^{Bt}z(0)\,</math> | |||
<math>e^{Bt}=\begin{bmatrix} | |||
e^{-5.2941t}&0&0&0 \\ | |||
0&e^{2.833it}&0&0 \\ | |||
0&0&e^{-2.83333it}&0 \\ | |||
0&0&0&e^{5.2941t} | |||
\end{bmatrix}\,</math> | |||
<math>x=T^{-1}z\,</math> | |||
<math>x=T^{-1}e^{Bt}Tx(0)\,</math> | |||
<math>e^{Pt}=T^{-1}e^{Bt}T\,</math> | |||
<math>e^{Pt}=\,</math>lots of variables | |||
'''Another way to solve using the Matrix exponential''' | |||
<math>e^{At}=\mathcal{L}^{-1}\left\{[SI-A]^{-1}\right\}\,</math> | |||
<math>[SI-A]\,</math> | |||
= | |||
<math> | |||
\begin{bmatrix} | |||
S&1&0&0 \\ | |||
\frac{(-50 N/m)}{15 kg}&S&\frac{-100 N/m}{15 kg}&0 \\ | |||
0&0&S&1 \\ | |||
\frac{100 N/m}{15 kg}&0&\frac{(250 N/m)}{15 kg}&S | |||
\end{bmatrix} | |||
</math> | |||
<math>[SI-A]^{-1} =\,</math> (something too large for my calculator to display or that I want to type out) | |||
<math>\mathcal{L}^{-1}\left\{[SI-A]^{-1}\right\} = \,</math>(something too large for my calculator to display or that I want to type out) | |||
Written by: Andrew Hellie | |||
Latest revision as of 22:28, 13 December 2009
Problem Statement
Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes of the system. Solve Using the Matrix Exponential
Initial Conditions:
F=ma
State Equations
=
With the numbers...
=
=
Eigenvalues
Eigenvectors
Standard Equation
Eigenmodes
- There are two eigenmodes for the system
- 1) m1 and m2 oscillating together
- 2) m1 and m2 oscillating at exactly a half period difference
Matrix Exponential using transformation z=Tx
lots of variables
Another way to solve using the Matrix exponential
=
(something too large for my calculator to display or that I want to type out)
(something too large for my calculator to display or that I want to type out)
Written by: Andrew Hellie