Chapter 2

Ideal Op Amp Characteristics

• Infinite input impedance
• Infinite open-loop gain for the differential signal
• Zero gain for the common mode signal
  • You can easily change an differential amplifier into a common-mode amplifier by grounding one of the inputs
• Zero output impedance
• Infinite bandwidth
  • To allow for infinite gain regardless of the frequency? Instantaneous feedback?

Op Amp Nodal Analysis

• No current flows into the + or - terminals
• If negative feedback is present (and no positive feedback), then $V_{+}=V_{-}\,$
• Write nodal equations at $V_{+}\,$ and $V_{-}\,$, but not at $V_{o}\,$
  • There is a voltage source inside the op amp. Writing a nodal equation at a voltage source adds an extra equation and an extra variable. You gain no ground.

DC imperfections

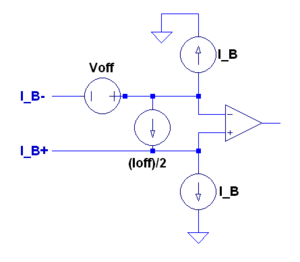
DC Imperfections

• Bias currents, $I_{B+}\,$ and $I_{B-}\,$, are the average dc currents flowing into the op amp input terminals. They can be caused by the signal source, feedback resistors, etc.
  • The bias current is the average of the dc currents. $I_{B}={\frac {I_{B+}+I_{B-}}{2}}$
• Offset current is the difference between the bias currents. $I_{off}=I_{B+}-I_{B-}\,$
• Offset voltage occurs when the output voltage is nonzero for zero input voltage.

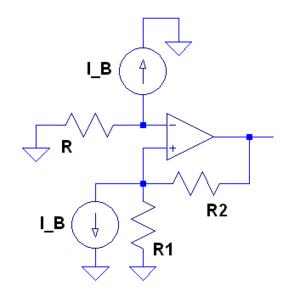
Canceling bias currents

• Because bias currents flow have equal magnitude and direction, it is possible to negate their effects.
  • The orientation of the offset voltage and the direction of the offset current are unknown, thus it is not possible to correct for these parameters with a circuit design.

Steps

1. Ground the input
2. Set the output to 0
3. Add in the bias currents
4. Add in the new resistor to balance out the
5. Set the two nodal equations equal to each other and solve for the new resistor

Problem 2.17

Problem 2.17 after finishing step 4

• Derive an expression for R in terms of the other resistor values, so that the output voltage due to the bias currents is zero.
• Solving the two nodal equations for the terminal voltage and then setting the two equations equal to each other gives: $-I_{B}R=-{\frac {I_{B}R_{2}R_{1}}{R_{1}+R_{2}}}$
• Solving for R gives: $R={\frac {R_{2}R_{1}}{R_{1}+R_{2}}}$