Fourier Series: Explained!: Difference between revisions
Michaelvier (talk | contribs) No edit summary |
John.hawkins (talk | contribs) No edit summary |
||
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
==A Brief Introduction== | |||
A Fourier series is a mathematical tool that takes a periodic function and turns it into a sum of simple oscillating functions (i.e. sines and cosines)<ref> [http://en.wikipedia.org/wiki/Fourier_series Fourier Series] </ref>. These series were discovered by Joseph Fourier to solve a heat equation in a metal plate. | A Fourier series is a mathematical tool that takes a periodic function and turns it into a sum of simple oscillating functions (i.e. sines and cosines)<ref> [http://en.wikipedia.org/wiki/Fourier_series Fourier Series]</ref>. These series were discovered by Joseph Fourier to solve a heat equation in a metal plate. | ||
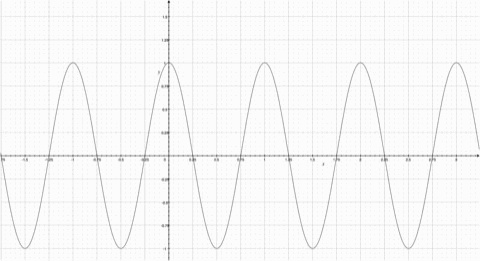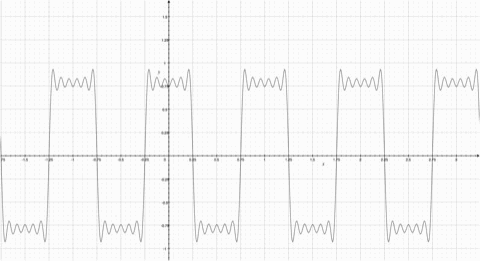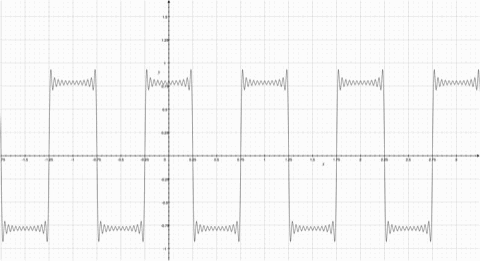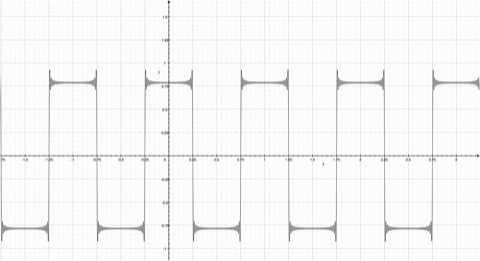
Fourier Series represents a periodic function through a sum of sines or cosines. Each term in the summation has a frequency n. The first term has the same frequency as the periodic function, the second term has twice the frequency of the periodic function, and so on. The more functions added, the more the summation resembles the step function. Observe the animation; notice how the summation function resembles the original periodic function more as more functions are added. | ==How They Work== | ||
[[Image:Square Wave.jpg| | A Fourier Series represents a periodic function through a sum of sines or cosines. Each term in the summation has a frequency n. The first term has the same frequency as the periodic function, the second term has twice the frequency of the periodic function, and so on. The more functions added, the more the summation resembles the step function. Observe the animation; notice how the summation function resembles the original periodic function more as more functions are added. | ||
[[Image:Square Wave.jpg|500px|thumb|right|Square Wave with similar periods to the cosine function]] | |||
[[Image:Fourier Animated.gif|500px|thumb|left|Fourier series animated to show increasing accuracy as evaluation bounds are increased.]] | [[Image:Fourier Animated.gif|500px|thumb|left|Fourier series animated to show increasing accuracy as evaluation bounds are increased.]] | ||
==References== | |||
<references/> | |||
==Helpful Links== | |||
[http://www.fourier-series.com/fourierseries2/flash_programs/fourier_series_sin_cos/index.html A very helpful game] | |||
==Contributors== | |||
*[[Lau, Chris | Christopher Garrison Lau I]] | |||
*[[Vier, Michael|Michael Vier]] | |||
==Reviewed By== | |||
*[[Grant, Joshua|Joshua Grant]] | |||
*[[Vazquez, Brandon]] | |||
==Read By== | |||
[[Hawkins, John]] | |||
Latest revision as of 03:12, 15 January 2010
A Brief Introduction
A Fourier series is a mathematical tool that takes a periodic function and turns it into a sum of simple oscillating functions (i.e. sines and cosines)<ref> Fourier Series</ref>. These series were discovered by Joseph Fourier to solve a heat equation in a metal plate.
How They Work
A Fourier Series represents a periodic function through a sum of sines or cosines. Each term in the summation has a frequency n. The first term has the same frequency as the periodic function, the second term has twice the frequency of the periodic function, and so on. The more functions added, the more the summation resembles the step function. Observe the animation; notice how the summation function resembles the original periodic function more as more functions are added.
References
<references/>