Example Problem - Toroid: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
'''Problem:''' |
'''Problem:''' |
||
Concerning Ampere's law |
|||
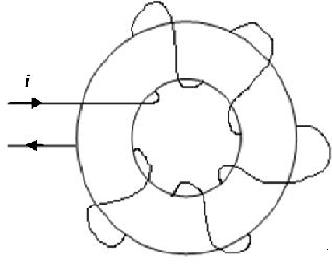
Let look at a coil around a toroid shown in the figure below. The coil has N = 20 turns around the toroid. The toroid has an inside diameter of ID = 4 cm and an outside diameter OD = 5 cm. Determine the field intensity H along the mean path length within the toroid with a current i = 2.5 A. |
Let look at a coil around a toroid shown in the figure below. The coil has N = 20 turns around the toroid. The toroid has an inside diameter of ID = 4 cm and an outside diameter OD = 5 cm. Determine the field intensity H along the mean path length within the toroid with a current i = 2.5 A. |
||
| Line 7: | Line 7: | ||
'''Solution:''' |
'''Solution:''' |
||
Do symmetry the magnetic field intensity Hm along a circular contour within the toroid is constant. We can find the radius by |
Do symmetry the magnetic field intensity Hm along a circular contour within the toroid is constant. We can find the mean radius by |
||
<math>r_m=(\frac{1}{2})\frac{OD + ID}{2}</math> |
<math>r_m=(\frac{1}{2})\frac{OD + ID}{2} = 2.25\ cm</math> |
||
Using the mean radius the mean path of length l_m can be calculated. |
|||
<math> l_m = { 2 \pi r_m} = 0.141\ </math> |
<math> l_m = { 2 \pi r_m} = 0.141\ </math> |
||
With Ampere's Law (below) the field intensity along the mean path can be Found. |
|||
<math>H_m=(\frac{Ni}{l_m})</math> |
<math>H_m=(\frac{Ni}{l_m})</math> |
||
Finally teh H_m can be calculated. |
|||
<math>H_m=\frac{20 x 2.5}{.141}= 354.6\ A /m)</math> |
<math>H_m=\frac{20 x 2.5}{.141}= 354.6\ A /m)</math> |
||
Since the width of the toroid is much smaller than the mean radius r_m we can assume a uniform H_m throughout teh cross-section of the toroid. |
|||
Revision as of 21:39, 18 January 2010
Problem: Concerning Ampere's law Let look at a coil around a toroid shown in the figure below. The coil has N = 20 turns around the toroid. The toroid has an inside diameter of ID = 4 cm and an outside diameter OD = 5 cm. Determine the field intensity H along the mean path length within the toroid with a current i = 2.5 A.
Solution:
Do symmetry the magnetic field intensity Hm along a circular contour within the toroid is constant. We can find the mean radius by
Using the mean radius the mean path of length l_m can be calculated.
With Ampere's Law (below) the field intensity along the mean path can be Found.
Finally teh H_m can be calculated.
Since the width of the toroid is much smaller than the mean radius r_m we can assume a uniform H_m throughout teh cross-section of the toroid.