Fourier Example: Difference between revisions

Latest revision as of 15:26, 25 January 2010

Find the Fourier Series of the function:

f (x) = {\begin{cases} 0, & - π \leq x < 0 \\ π, & 0 \leq x \leq π \end{cases}

Here we have

$a_{o} = \frac{1}{2 π} (\int_{- π}^{0} 0 d x + \int_{0}^{π} π d x) = \frac{π}{2}$

$a_{n} = \int_{0}^{π} π c o s (n x) d x = 0, n \geq 1,$

and

b_{n} = \int_{0}^{π} π \sin (n x) d x = \frac{1}{n} (1 - c o s (x π)) = \frac{1}{n} (1 - (- 1)^{n})

We obtain $b_{2 n}$ = 0 and

$b_{2 n + 1} = \frac{2}{2 n + 1}$

Therefore, the Fourier series of f(x) is

$f (x) = \frac{π}{2} + 2 (s i n (x) + \frac{s i n (3 x)}{3} + \frac{s i n (5 x)}{5} + . . .)$

@@ Line 1: / Line 1: @@
 Find the Fourier Series of the function:
-<br />
-<center><math>\f(x)=begin{cases}
+:<math>f(x) = \begin{cases}0,& -\pi\le x<0\\
+\pi,& 0 \le x \le \pi\\
+\end{cases}</math>
-,-pi<x<0
-\end{cases} \ \ \ \ n=0,1,2,3\dots</math></center>
-<br />
-:<math>\rho_X(x) = \begin{cases}\frac{1}{2},& \x=0,\\
+== Solution ==
-\frac{1}{2},& \x=1,\\
-,& \text{otherwise} .\end{cases}</math>
- <!--  -->
+Here we have
+<math>a_o=\frac{1}{2\pi}(\int_{-\pi}^00\ dx+\int_{0}^\pi\pi\ dx)=\frac{\pi}{2}</math>
+<math>a_n=\int_{0}^\pi\pi cos(nx)\ dx=0,   n\ge1,</math>
+and
+:<math>b_n = \int_{0}^\pi  \pi\sin(nx)\, dx = \frac{1}{n}(1-cos(x\pi))=\frac{1}{n}(1-(-1)^n)</math>
+We obtain   <math>b_{2n}</math> = 0 and
+<math>b_{2n+1}=\frac{2}{2n+1}</math>
+Therefore, the Fourier series of f(x) is
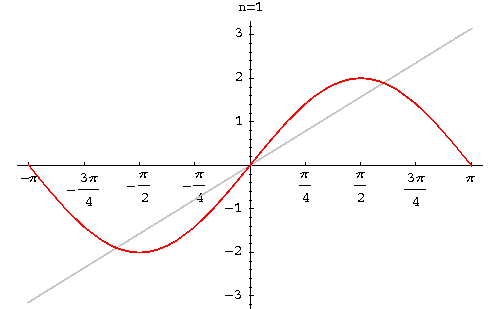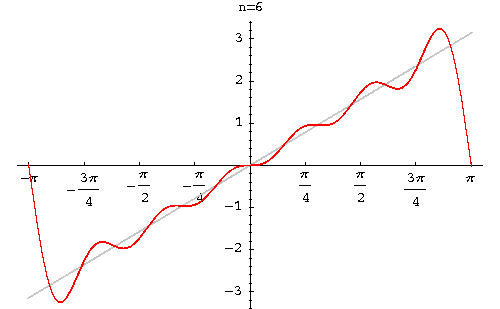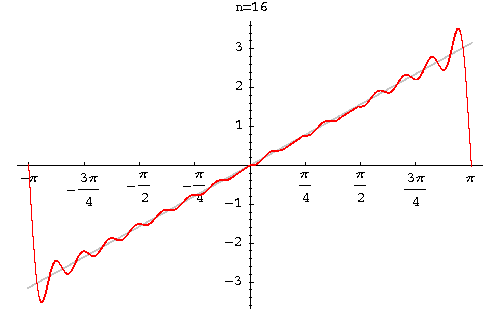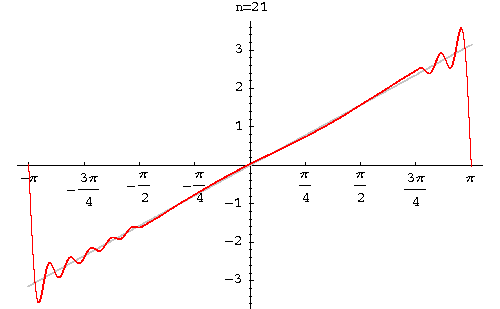
+<math>f(x)=\frac{\pi}{2}+2(sin(x)+\frac{sin(3x)}{3}+\frac{sin(5x)}{5}+...)</math>
+==Solution Graph==
+[[Image:Fourier.gif]]
+==***BONUS*** VIDEO! (For people completely lost on Fourier Series)==
+http://www.youtube.com/watch?v=nXEqrOt-nB8
+==References:==
+[[Fourier Series: Basic Results]]
+==Readers==
+[[Lau, Chris|Christopher Garrison Lau I]]