Transformer example problem: Difference between revisions
No edit summary |
|||
| (53 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
===Problem:=== | ===Problem:=== | ||
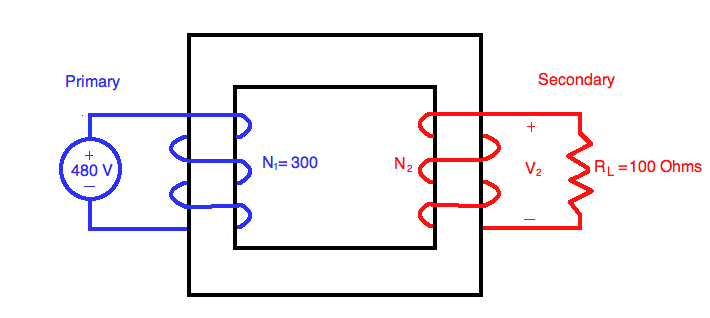
An ideal transformer with a 300 turn primary connected to a 480 V, 60 Hz supply line | An ideal transformer with a 300 turn primary connected to a 480 V, 60 Hz supply line needs to output 120 V from the secondary. If a 100 Ω resistor is connected across the secondary, determine: A) How many turns the secondary must have to output the desired voltage. B) The current through the resistor, C)The current drawn through the primary. D) The maximum flux in the core of the transformer | ||
[[Image:Transformer_EMEC.png]] | |||
===Solution:=== | ===Solution:=== | ||
| Line 16: | Line 18: | ||
<math>\frac{480 \ volts}{120 \ volts} = \frac{300 turns}{N_2}</math> | <math>\frac{480 \ volts}{120 \ volts} = \frac{300 \ turns}{N_2}</math> | ||
<br/> | <br/> | ||
<br/> | <br/> | ||
To solve for the number of turns required for the secondary, the equation is rearranged solving for N_2: | To solve for the number of turns required for the secondary, the equation is rearranged solving for <math>N_2 = </math>: | ||
<br/> | <br/> | ||
<br/> | <br/> | ||
| Line 25: | Line 27: | ||
====Part B:==== | ====Part B:==== | ||
The voltage across the secondary is given in the problem statement as 120 volts. Using ohms law, <math> V =i \cdot R </math>, we can solve for the current. | The voltage across the secondary is given in the problem statement as 120 volts. Using ohms law, <math> V =i \cdot R </math>, we can solve for the current in the loop (<math> i_2 </math> ). | ||
<br/> | <br/> | ||
<math> i_2 = \frac{V_2}{R_L}</math> | <math> i_2 = \frac{V_2}{R_L}</math> | ||
| Line 31: | Line 33: | ||
Where <math> i_2 = </math> Current through secondary, | Where <math> i_2 = </math> Current through secondary, | ||
<math>V_2 = </math>Voltage across secondary, | <math>V_2 = </math>Voltage across secondary, | ||
<math>R_L = </math> Load Resistor (R_L = 100 Ω) | <math>R_L = </math> Load Resistor (<math>R_L = </math> 100 Ω) | ||
<br/> | <br/> | ||
<br/> | <br/> | ||
| Line 37: | Line 39: | ||
====Part C:==== | ====Part C:==== | ||
The ratio of primary current to secondary current is inversely proportional to the ratio of number of turns on the primary to number of turns on the secondary: | |||
<br/> | |||
<br/> | |||
<math>\frac{i_1}{i_2} = \frac{N_2}{N_1}</math> | |||
<br/> | |||
Where <math> i_1 = </math>Current in primary, | |||
<math>i_2 = </math>Current in secondary, | |||
<math>N_1 = </math> Number of turns in primary, | |||
<math>N_2 = </math> Number of turns in secondary | |||
<math>\frac{i_1}{1.2 \ A} = \frac{75 \ turns}{300 \ turns}</math> | |||
Rearranging to solve for <math>i_1 </math>: | |||
<math>\ i_1 = i_2 \cdot \frac{N_2}{N_1} \Rightarrow 1.2 A \cdot \frac{75 \ turns}{300 \ turns} \Rightarrow i_1 = .3 \ A</math> | |||
====Part D:==== | |||
The induced emf of the secondary can be calculated by: | |||
<math> V_2 = 4.44 \ \cdot \mathit{f} \cdot N_2 \cdot \Phi_m \ \angle 0^\circ </math><ref>Guru and Huseyin, ''Electric Machinery and Transformers'', 3rd ed. (New York: Oxford University Press, 2001), 209.</ref> | |||
Solving for <math> \Phi_m </math>, we can calculate the maximum flux in the core: | |||
<math> \ \Phi_m = \frac{V_2}{4.44 \cdot \mathit{f} \cdot N_2} </math> | |||
Where <math> \Phi_m \ = </math>max flux in core, | |||
<math>V_2 = </math>Voltage across secondary, | |||
<math>\mathit{f} = </math> Frequency of line, | |||
<math>N_2 = </math> Number of turns in secondary | |||
<math> \ \Phi_m = \frac{120}{4.44 \cdot 60 \ Hz \cdot 75} \Rightarrow \Phi_m = 6.006 \ mWb </math> | |||
*Comment: There is a problem here in Part D, because in an ideal transformer <math>N_1 I_1 = N_2 I_2</math> and the flux from <math>I_2</math> opposes the flux from <math>I_1</math>. Magnetic circuits tells us that the flux, <math>\Phi_1 = \frac{ N_1 I_1 } \mathcal{R} </math>and the flux, <math>{\Phi_2} = \frac{-N_2 I_2} {\mathcal{R}}</math> so that the total flux in any ideal transformer is zero. | |||
==References:== | |||
<references/> | |||
==Authors:== | |||
[[Tim Rasmussen]] | |||
==Reviewers:== | |||
Wesley Brown | |||
Alex Roddy | |||
==Readers:== | |||
Latest revision as of 12:25, 4 February 2010
Problem:
An ideal transformer with a 300 turn primary connected to a 480 V, 60 Hz supply line needs to output 120 V from the secondary. If a 100 Ω resistor is connected across the secondary, determine: A) How many turns the secondary must have to output the desired voltage. B) The current through the resistor, C)The current drawn through the primary. D) The maximum flux in the core of the transformer
Solution:
Part A:
The ratio of primary voltage to secondary voltage is directly proportional to the ratio of number of turns on the primary to number of turns on the secondary:
Where Voltage across primary,
Voltage across secondary,
Number of turns in primary,
Number of turns in secondary
To solve for the number of turns required for the secondary, the equation is rearranged solving for :
Part B:
The voltage across the secondary is given in the problem statement as 120 volts. Using ohms law, , we can solve for the current in the loop ( ).
Where Current through secondary,
Voltage across secondary,
Load Resistor ( 100 Ω)
Part C:
The ratio of primary current to secondary current is inversely proportional to the ratio of number of turns on the primary to number of turns on the secondary:
Where Current in primary,
Current in secondary,
Number of turns in primary,
Number of turns in secondary
Rearranging to solve for :
Part D:
The induced emf of the secondary can be calculated by: <ref>Guru and Huseyin, Electric Machinery and Transformers, 3rd ed. (New York: Oxford University Press, 2001), 209.</ref> Solving for , we can calculate the maximum flux in the core:
Where max flux in core, Voltage across secondary, Frequency of line, Number of turns in secondary
- Comment: There is a problem here in Part D, because in an ideal transformer and the flux from opposes the flux from . Magnetic circuits tells us that the flux, and the flux, so that the total flux in any ideal transformer is zero.
References:
<references/>
Authors:
Reviewers:
Wesley Brown
Alex Roddy