Example: Metal Cart: Difference between revisions
Amy.crosby (talk | contribs) No edit summary |
|||
| (17 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
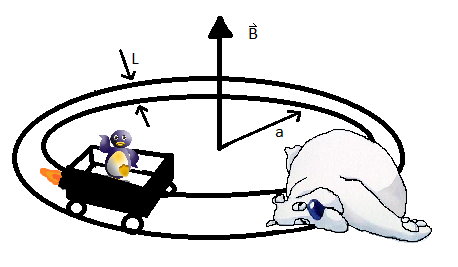
A DC generator is built using a metal cart with metallic wheels that travel around a set of perfectly conducting rails in a large circle. The rails are L m apart and there is a uniform magnetic <math>\vec B</math> field normal to the plane. The cart has a penguin, | A DC generator is built using a metal cart with metallic wheels that travel around a set of perfectly conducting rails in a large circle. The rails are L m apart and there is a uniform magnetic <math>\vec B</math> field normal to the plane. The cart has a penguin,with mass m, and is driven by a rocket engine having a constant thrust <math> F_1 </math>. A wet polar bear, having stumbled out of a shack where he recently had a bad experience with a battery, lays dying across the tracks acting as a load resistance R over the rails. Find The current as a function of time. What is the current after the generator attains the steady-state condition? | ||
[[Image:Emec_cart_polarBear2.png]] | [[Image:Emec_cart_polarBear2.png]] | ||
<blockquote>Problem loosely based on 2.6 from Electric Machinery and Transformers, 3rd ed | |||
<ref>Guru and Huseyin, ''Electric Machinery and Transformers'', 3rd ed. (New York: Oxford University Press, 2001)</ref></blockquote> | |||
==Solution== | ==Solution== | ||
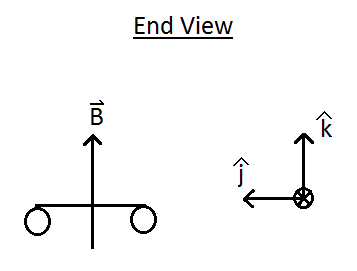
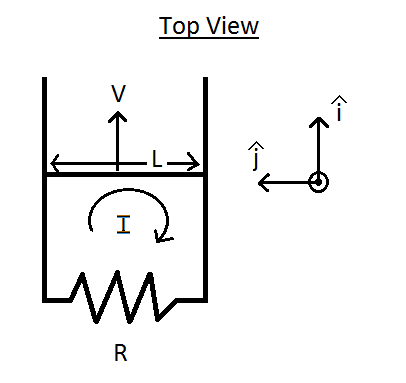
For this Problem | For this Problem the large circle will be represented by a pair of parallel wires and the cart as a single wire. This is illustrated below in the top and end view figures. | ||
[[Image:Emec_cart_topview.png]] | [[Image:Emec_cart_topview.png]] | ||
| Line 68: | Line 70: | ||
<math> I(t)=\frac{\frac {F_0~R}{L~B}\left(1~-~e^{-\frac{L^2~B^2}{R ~m}~t}\right)}{R}~~~~~\Longrightarrow~~~~~ I(t)~=~\frac {F_0}{L~B}\left(1~-~e^{-\frac{L^2~B^2}{R ~m}~t}\right)</math> | <math> I(t)=\frac{\frac {F_0~R}{L~B}\left(1~-~e^{-\frac{L^2~B^2}{R ~m}~t}\right)}{R}~~~~~\Longrightarrow~~~~~ I(t)~=~\frac {F_0}{L~B}\left(1~-~e^{-\frac{L^2~B^2}{R ~m}~t}\right)</math> | ||
To find the steady-state current we simply look at the limit of I(t) as <math> | To find the steady-state current we simply look at the limit of I(t) as <math>t \rightarrow \infty</math> | ||
<math>\lim_{t\rightarrow \infty} I(t)=\frac{F_0}{L~B} \left( 1- e^{-\infty}\right) ~~~~~\Longrightarrow~~~~~ I(\infty)=\frac{F_0}{L~B} </math> | |||
So the Steady-State Current = <math>\frac{F_0}{L~B}</math> | |||
In conclusion it can be seen that a penguin driven, polar bear killing generator would be a viable option for alternative energy in Canada. | |||
<math> In~conclusion~it ~can ~be ~seen ~that ~a ~penguin ~driven, ~polar ~bear ~killing ~generator </math> | |||
<math>~would ~be ~a ~viable ~option ~for ~alternative ~energy ~in ~Canada. </math> | |||
==References== | |||
<references /> | |||
==Reviewed by== | |||
[[Kirk Betz]] Read and approved 1-26-10 | |||
[[Will Griffith]] Approved 1-27-10 | |||
==Read By== | |||
==Comments== | |||
*I completely agree with your conclusion (Tim Rasmussen) | |||
*I'm just worried about the ecologists. (J. Apablaza) | |||
Latest revision as of 19:44, 15 February 2010
Problem
A DC generator is built using a metal cart with metallic wheels that travel around a set of perfectly conducting rails in a large circle. The rails are L m apart and there is a uniform magnetic field normal to the plane. The cart has a penguin,with mass m, and is driven by a rocket engine having a constant thrust . A wet polar bear, having stumbled out of a shack where he recently had a bad experience with a battery, lays dying across the tracks acting as a load resistance R over the rails. Find The current as a function of time. What is the current after the generator attains the steady-state condition?
Problem loosely based on 2.6 from Electric Machinery and Transformers, 3rd ed <ref>Guru and Huseyin, Electric Machinery and Transformers, 3rd ed. (New York: Oxford University Press, 2001)</ref>
Solution
For this Problem the large circle will be represented by a pair of parallel wires and the cart as a single wire. This is illustrated below in the top and end view figures.
We have two forces, being the force from the rocket engine and being the force caused by the current in the conductor and the Magnetic Field. The resulting Force is simply the sum of and
can be found using Ampere's Law
We can also say that
And
Now we have a lovely differential equation to work with! To attempt to find the current we will take the Laplace transform.
Lets title and substitute in the variable to simplify things
Using partial fraction expansion
We know that
So we can substitute in V(t) to get
And we know that
To find the steady-state current we simply look at the limit of I(t) as
So the Steady-State Current =
References
<references />
Reviewed by
Kirk Betz Read and approved 1-26-10
Will Griffith Approved 1-27-10
Read By
Comments
- I completely agree with your conclusion (Tim Rasmussen)
- I'm just worried about the ecologists. (J. Apablaza)