Matlab or Octave Script for this problem.: Difference between revisions

From Class Wiki
Jump to navigation Jump to search
(New page: % This octave/Matlab script demonstrates the state space model of the J=0.01; b=0.1; K=0.01; R=1; L=0.5; A1=[[0,1,0];[0,-b/J,K/J];[0,-K/L,-R/L]]; B1=[0,0,1/L]'; C1=[0,1,0]; % The outp...)
 
No edit summary
 
(7 intermediate revisions by the same user not shown)
Line 1: Line 1:
% This octave/Matlab script demonstrates the state space model of the
% This octave/Matlab script demonstrates the state space model of the

J=0.01;
J=0.01;
b=0.1;
b=0.1;
K=0.01;
K=0.01;
R=1;
R=1;
L=0.5;
L=0.5;
A1=[[0,1,0];[0,-b/J,K/J];[0,-K/L,-R/L]];
A1=[[0,1,0];[0,-b/J,K/J];[0,-K/L,-R/L]];
B1=[0,0,1/L]';
B1=[0,0,1/L]';
C1=[0,1,0]; % The output is the angular velocity omega.
C1=[0,1,0]; % The output is the angular velocity omega.
sys1=ss(A1,B1,C1); % Note that theta cannot be controlled.
sys1=ss(A1,B1,C1); % Note that theta cannot be controlled.
% There is a warning in octave from this.
% So we use only the theta dot, and i_a as state variables.
% So we use only the theta dot, and i_a as state variables.
A2=[[-b/J, K/J];[-K/L,-R/L]];
B2=[0,1/L]';
A2=[[-b/J, K/J];[-K/L,-R/L]];
C2=[1,0];
B2=[0,1/L]';
C2=[1,0];
sys2=ss(A2,B2,C2);
sys2=ss(A2,B2,C2);
figure(1)
figure(1)
clf;
clf;

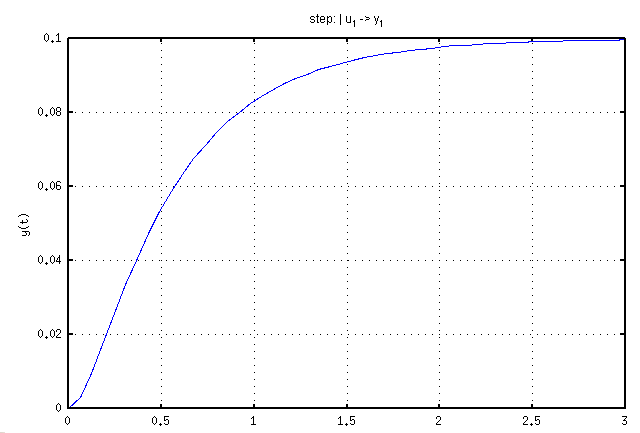
Here is the unit step response for <math>\omega</math> or angular velocity as a function of time.

[[Image:Step_response_dc_motor.png]]

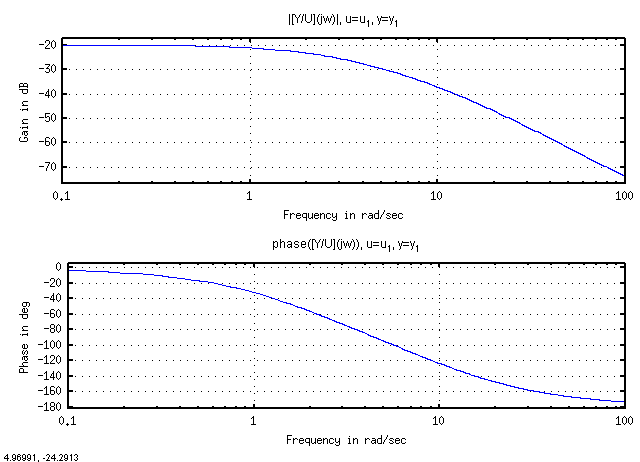
Here is the system response with the output being <math>\omega</math> and the input being the input voltage.

[[Image:Bode_Plot_DC_Motor.png]]

Latest revision as of 11:50, 10 March 2010

% This octave/Matlab script demonstrates the state space model of the 
J=0.01;
b=0.1;
K=0.01;
R=1;
L=0.5;
A1=[[0,1,0];[0,-b/J,K/J];[0,-K/L,-R/L]];
B1=[0,0,1/L]';
C1=[0,1,0]; % The output is the angular velocity omega.
sys1=ss(A1,B1,C1);  % Note that theta cannot be controlled.
% There is a warning in octave from this.
% So we use only the theta dot, and i_a as state variables.
A2=[[-b/J, K/J];[-K/L,-R/L]];
B2=[0,1/L]';
C2=[1,0];
sys2=ss(A2,B2,C2);
figure(1)
clf;

Here is the unit step response for or angular velocity as a function of time.

Step response dc motor.png

Here is the system response with the output being and the input being the input voltage.

Bode Plot DC Motor.png

Retrieved from "http:///class-wiki/index.php?title=Matlab_or_Octave_Script_for_this_problem.&oldid=9227"