Matlab or Octave Script for this problem.: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 18: | Line 18: | ||
clf; | clf; | ||
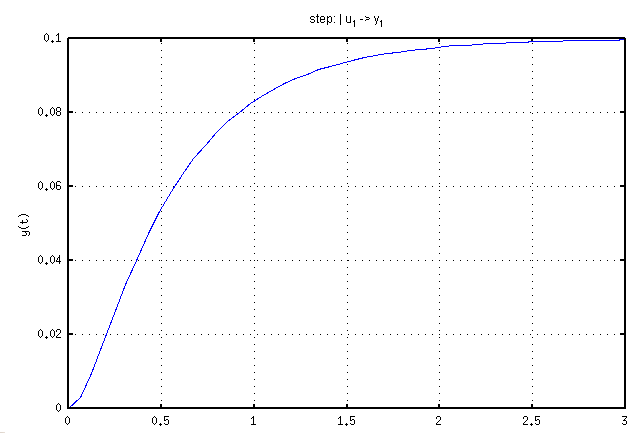
Here is the unit step response for <math>\omega</math> or angular velocity as a function of time. | |||
[[Image:Step_response_dc_motor.png | [[Image:Step_response_dc_motor.png]] | ||
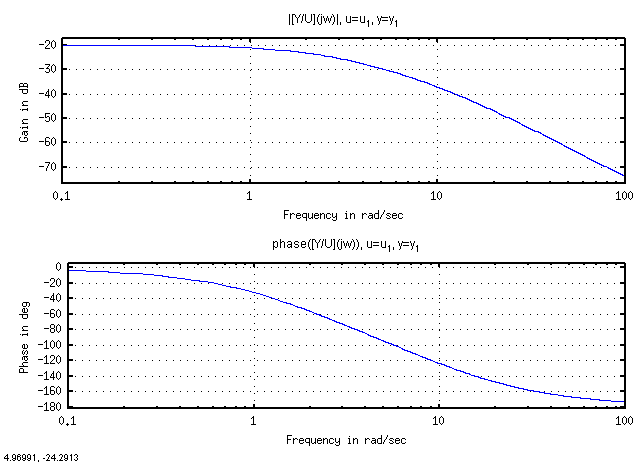
Here is the system response with the output being <math>\omega</math> and the input being the input voltage. | |||
[[Image:Bode_Plot_DC_Motor.png]] | |||
Latest revision as of 11:50, 10 March 2010
% This octave/Matlab script demonstrates the state space model of the J=0.01; b=0.1; K=0.01; R=1; L=0.5; A1=[[0,1,0];[0,-b/J,K/J];[0,-K/L,-R/L]]; B1=[0,0,1/L]'; C1=[0,1,0]; % The output is the angular velocity omega. sys1=ss(A1,B1,C1); % Note that theta cannot be controlled. % There is a warning in octave from this. % So we use only the theta dot, and i_a as state variables. A2=[[-b/J, K/J];[-K/L,-R/L]]; B2=[0,1/L]'; C2=[1,0]; sys2=ss(A2,B2,C2); figure(1) clf;
Here is the unit step response for or angular velocity as a function of time.
Here is the system response with the output being and the input being the input voltage.