Christman GeneralizedReceiver

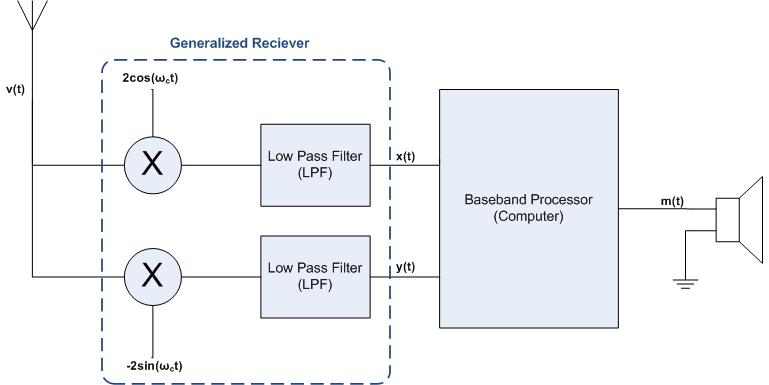
How It Works: Generalized Receiver

The process of transmitting data, $m(t)$, via a wireless signal, $v(t)$, is shown below:

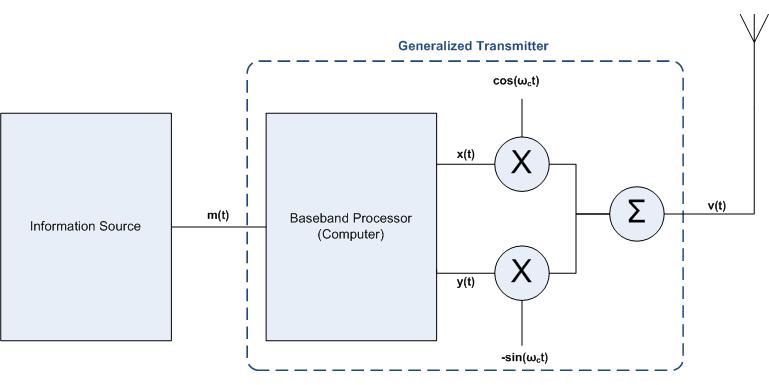
As can be seen from the figure above, in order to transmit $m(t)$, one must first process the data using a baseband processor (usually accomplished with software). As a result of this process the original data will be split into two signals, $x(t)$ and $y(t)$. Why is this you ask? In the world of "Communication Systems" a signal to be transmitted can be written as

$\displaystyle v(t)=Re[g(t)\cdot e^{j\omega _{c}t}]$,

where $g(t)=x(t)+jy(t)$ is the signal to be sent and $\scriptstyle e^{j\omega _{c}t}=\cos {\omega _{c}t}+j\sin {\omega _{c}t}$ (Euler's identity) shifts the signal in the frequency domain by $\omega _{c}=2\pi f_{c}$.
The above formula can then be rewritten to obtain the following relationship:

$\displaystyle v(t)=Re[g(t)\cdot e^{j\omega _{c}t}]=Re[(x(t)+jy(t))\cdot (\cos {\omega _{c}t}+j\sin {\omega _{c}t})=x(t)\cos {\omega _{c}t}-y(t)\sin {\omega _{c}t}$.

To visualize this process, observe the following figure:
This is why it is necessary to split $m(t)$ into the the two signals $x(t){\text{ and }}y(t)$. As you can also from the above relationship, in order to obtain the appropriate output signal $v(t)$ one must multiply $x(t)$ by a cosine function and $y(t)$ by a negative sine function and then sum the results (this is illustrated in the figure above). In simplified terms and details, this is essentially how the data $m(t)$ is transmitted. The process of receiving the data is very similar, as is described below.