Christman GeneralizedReceiver

How It Works: Generalized Receiver

The process of transmitting data, $m(t)$, via a wireless signal, $v(t)$, is shown below:

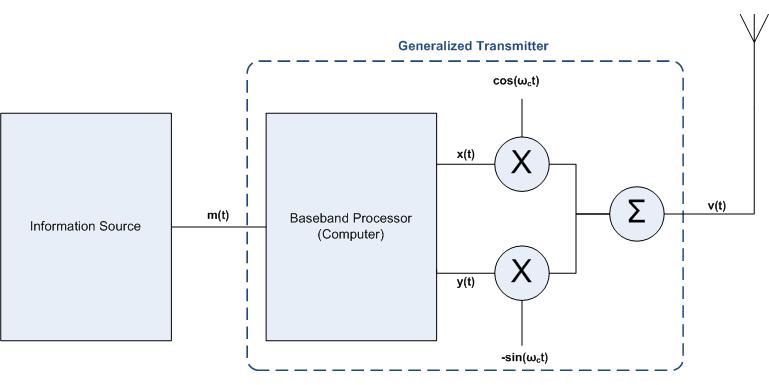
As can be seen from the figure above, in order to transmit $m(t)$, one must first process the data using a baseband processor (usually accomplished with software). As a result of this process the original data will be split into two signals, $x(t)$ and $y(t)$, and shifted to a frequency $f_{c}$ (and $-f_{c}$ because of the notion of a complex conjugate). Note that the original wireless communication data that you want to send is in the form known as baseband, which consists of frequencies near D.C. (or $f_{c}=0$). When you actually send the communication data, however, you want to send it via much higher frequency (one which is inaudible to humans) and this creates a bandpass signal. This concept is illustrated below:

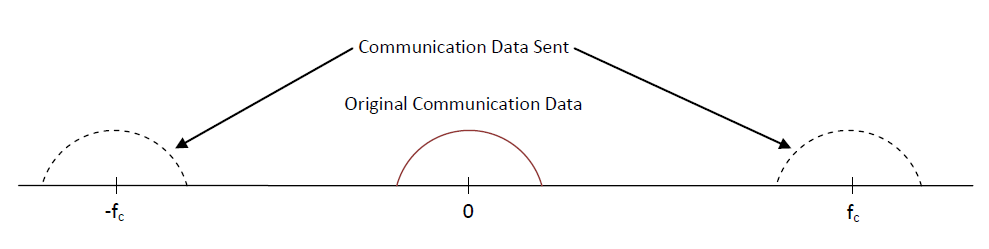
How is the data split and shifted you ask? Mathematically speaking, in the world of "Communication Systems" a signal to be transmitted can be written as

$\displaystyle v(t)=Re[g(t)\cdot e^{j(\omega _{c}t)}]$,

where $g(t)=x(t)+jy(t)$ is the signal to be sent and $\scriptstyle e^{j\omega _{c}t}=\cos {(\omega _{c}t)}+j\sin {(\omega _{c}t)}$ (Euler's identity) shifts the signal in the frequency domain by $\omega _{c}=2\pi f_{c}$.
The above formula can then be rewritten to obtain the following relationship:

$\displaystyle v(t)=Re[g(t)\cdot e^{j\omega _{c}t}]=Re[(x(t)+jy(t))\cdot (\cos {(\omega _{c}t)}+j\sin {(\omega _{c}t)})]=x(t)\cos {(\omega _{c}t)}-y(t)\sin {(\omega _{c}t)}$.

As you can also see from the above relationship, in order to obtain the appropriate output signal $v(t)$ one must multiply $x(t)$ by a cosine function and $y(t)$ by a negative sine function and then sum the results (this is illustrated in the figure above). In simplified terms and details, this is essentially how the data $m(t)$ is transmitted.

Receiving the original data from a wireless signal is very similar to that of transmitting the data (as described before). The process of receiving data, $m(t)$, via a wireless signal, $v(t)$, is shown below:

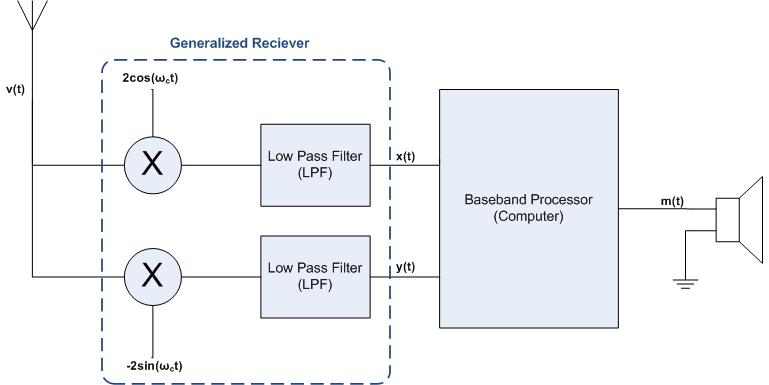
In short, the data that we are interested in ($m(t)$) is embedded within the carrying signal ($v(t)$) which is at a frequency inaudible to human ears. Thus, in order to get the original communication data it is necessary to somehow bring the bandpass signal back down to its original baseband form -- and this is what the second quarter of electronics is all about. If you have not already discovered, to recover the original data $x(t)$ and $y(t)$ from the signal signal $v(t)$ we must perform a task known as "mixing" and then run the results through low pass filters. Simply put, we need to multiply $v(t)$ by $2\cdot \cos {(\omega _{c}t)}$ and $-2\cdot \sin {(\omega _{c}t)}$ (the "$2$" is not necessary, but it makes the math a little nicer in the end). To see this mathematically, recall that $v(t)=x(t)\cos {(\omega _{c}t)}-y(t)\sin {(\omega _{c}t)}$. Therefore,

$2\cos {(\omega _{c}t)}\cdot v(t)=2cos{(\omega _{c}t)}\cdot [x(t)\cos {(\omega _{c}t)}-y(t)\sin {(\omega _{c}t)}]=2x(t)\cos ^{2}{(\omega _{c}t)}-2y(t)\cos {(\omega _{c}t)}\sin {(\omega _{c}t)}$

Using the trigonometric identities

$\cos ^{2}{\theta }={\frac {1+\cos {2\theta }}{2}}$

and

$\cos {\theta }\sin {\theta }={\frac {1}{2}}\sin {\theta }$,

we can see that

$\displaystyle 2x(t)\cos ^{2}{(\omega _{c}t)}-2y(t)\cos {(\omega _{c}t)}\sin {(\omega _{c}t)}=x(t)+x(t)\cos {(2\omega _{c}t)}-y(t)\sin {(2\omega _{c}t)}$.

But when this result is ran through a low pass filter it is fairly obvious that $x(t)\cos {(2\omega _{c}t)}-y(t)\sin {(2\omega _{c}t)}$ is filtered out (because of the $2\omega _{c}$), but $x(t)$ is unaltered by the filter (because it is independent of frequency); therefore, we are left with $x(t)$ as desired! (Similarly, $y(t)$ can be obtained.) This is essentially how a generalized receiver functions: given a bandpass signal, $v(t)$, and we can use a mixer and low pass filters to obtain an original baseband signal, $m(t)$ (in the form of $x(t)$ and $y(t)$, of course).

---

Please feel free to fix any mistakes. Please list your name, date fixed, and short description below.

• Name, Date, Description