Robert's HW: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 3: | Line 3: | ||
Assume a boat of arbitrary geometry, with a given displacement(weight) D, mass moment of inertia I, and metacentric height GM (The metacenter is a theoretical point in a boat through which the buoyant force always passes for small angles of list.). | Assume a boat of arbitrary geometry, with a given displacement(weight) D, mass moment of inertia I, and metacentric height GM (The metacenter is a theoretical point in a boat through which the buoyant force always passes for small angles of list.). | ||
[[Image: | [[Image:Righting_arm.png|thumb|right|500px|]] | ||
As the boat lists at angle φ, the centroid of the displaced volume of water shifts in the same direction, causing the buoyant force to be offset, resulting in a moment acting to right the boat. This righting moment is equal to the displacement of the boat times the righting arm GZ, where: | As the boat lists at angle φ, the centroid of the displaced volume of water shifts in the same direction, causing the buoyant force to be offset, resulting in a moment acting to right the boat. This righting moment is equal to the displacement of the boat times the righting arm GZ, where: | ||
| Line 38: | Line 33: | ||
<math> \varphi(t)= \mathcal{L}^{-1} \{ \Phi(s) \} = \varphi_0 cos \left( - \dfrac{ (D) (GM) }{I} t \right)u(t) </math> | <math> \varphi(t)= \mathcal{L}^{-1} \{ \Phi(s) \} = \varphi_0 cos \left( - \sqrt{\dfrac{ (D) (GM) }{I}} t \right)u(t) </math> | ||
This implies that, like a pendulum, a boat has a natural period of oscilation determined only by it's own physical properties. This period is important when considering more dynamic problems such as the motion of a boat in a storm. | This implies that, like a pendulum, a boat has a natural period of oscilation determined only by it's own physical properties. This period is important when considering more dynamic problems such as the motion of a boat in a storm. | ||
Latest revision as of 15:51, 1 November 2010
I decided to model the natural response of a boat given a small initial list on flat water.
Assume a boat of arbitrary geometry, with a given displacement(weight) D, mass moment of inertia I, and metacentric height GM (The metacenter is a theoretical point in a boat through which the buoyant force always passes for small angles of list.).
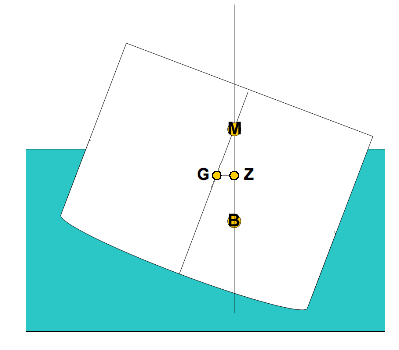
As the boat lists at angle φ, the centroid of the displaced volume of water shifts in the same direction, causing the buoyant force to be offset, resulting in a moment acting to right the boat. This righting moment is equal to the displacement of the boat times the righting arm GZ, where:
GZ = GM*sin φ
Which at small angles of φ can be approximated:
GZ = GM*φ
Thus, summing moments about the center of gravity of the boat:
Rearranging:
This is a simple ODE that may be solved using Laplace transforms.
Solving for :
Assuming no initial angular velocity () and converting back to time domain:
This implies that, like a pendulum, a boat has a natural period of oscilation determined only by it's own physical properties. This period is important when considering more dynamic problems such as the motion of a boat in a storm.