Andy's Fourier Series Project: Difference between revisions
| Line 37: | Line 37: | ||
</math> |
</math> |
||
Where k = spring constant and that is assumed to be 70560. |
Where k = spring constant and that is assumed to be 70560 and the mass = 2500 lbm. |
||
<math>\begin{align} |
<math>\begin{align} |
||
x(t) = c_1 cos |
x(t) = c_1 cos\frac{sqrt(k) t)}{sqrt(m)}+c_2 sin\frac{sqrt(k) t}{sqrt(m)}\\ |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
Revision as of 18:59, 1 November 2010
Damped Spring Mass With Dash Pot
Project Statement
I chose to analyze a car's suspension. Only one wheel's system will be considered to simplify calculations. The car will be simulated as running over a constant road surface similar to that of an ideal driving surface. The Fourier series can be represented with proper assumptions. A coil spring will be considered.
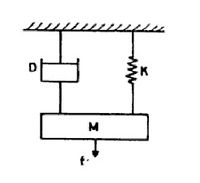
First a picture to represent the system used in a car.
D = Dash pot (shock absorber)
K = spring
M = mass of 1/4 of the car
To imagine this system accurately we must flip the diagram upside-down and the ground can then be the road and the mass (M) and the force of the car (f) can be in the proper direction. To find the Fourier series the Dash pot (D) will be neglected. The Dash pot will be implemented later to show the effectiveness of the car's suspension to slow the wave motion caused by road surfaces.
Analysis
These are the equations of Fourier Series:
The equation of motion is to be considered:
Where k = spring constant and that is assumed to be 70560 and the mass = 2500 lbm.