User talk:Gregory.peterson: Difference between revisions
Jump to navigation
Jump to search
| (5 intermediate revisions by 2 users not shown) | |||
| Line 103: | Line 103: | ||
<math>\mathbf {X}(s)=-\frac{4}{(s+2)^2} </math><br /><br /> | <math>\mathbf {X}(s)=-\frac{4}{(s+2)^2} </math><br /><br /> | ||
===Bode Plot=== | |||
<math>\text {This plot is done using the control toolbox in MatLab. }\,</math> | |||
[[Image:bodeplotlna.jpeg|700px|thumb|left|Fig (1)]] | |||
Created by Greg Peterson | |||
Checked by Mark Bernet | |||
Latest revision as of 14:51, 27 October 2009
Using the Laplace Transform to solve a spring mass system that is critically damped
Problem Statement
An 98 Newton weight is attached to a spring with a spring constant k of 40 N/m. The spring is stretched 4 m and rests at its equilibrium position. It is then released from rest with an initial upward velocity of 2 m/s. The system contains a damping force of 40 times the initial velocity.
Solution
Given
Solving the problem
Apply the Initial and Final Value Theorems to find the initial and final values
- Initial Value Theorem
- Final Value Theorem
Applying this to our problem
Bode Plot of the transfer function
Transfer Function
Bode Plot
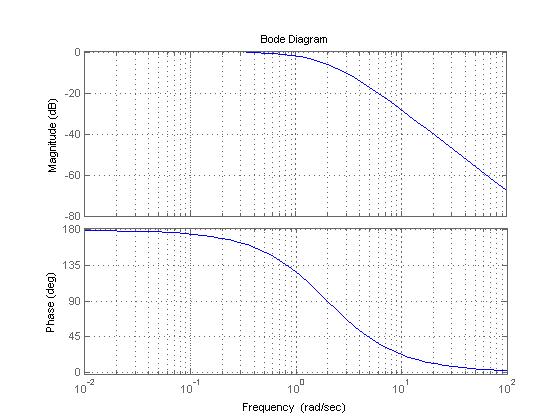
Created by Greg Peterson
Checked by Mark Bernet