Quadrature sampling waveform plot - HW10: Difference between revisions
Jump to navigation
Jump to search
Max.Woesner (talk | contribs) New page: == Max Woesner == Back to my Home Page === Homework #10 - Quadrature sampling waveform plot === <br><b>Problem Statement</b><br><br> Plot <math> \ \frac{2}{T} \sum_{n=1}^... |
Max.Woesner (talk | contribs) No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 7: | Line 7: | ||
Plot <math> \ \frac{2}{T} \sum_{n=1}^\infty sin\bigg(\frac{2 \pi nt}{T}\bigg) \!</math><br><br> | Plot <math> \ \frac{2}{T} \sum_{n=1}^\infty sin\bigg(\frac{2 \pi nt}{T}\bigg) \!</math><br><br> | ||
<b>Solution</b><br> | <b>Solution</b><br> | ||
While we can't sum to infinity in the computer, we can get a close approximation summing over a large enough range of <math> n \!</math><br> | |||
I found summing over <math> n = 1:1000 \!</math> was about the most the computer could handle reasonably.<br> | |||
The following script was written in MATLAB to produce the desired plot. <br> | |||
<pre> | |||
clear all; | |||
close all; | |||
sum = 0; | |||
T = 1; | |||
t = -T:0.0001:T; | |||
N = 1000; | |||
for n = 1:N; | |||
if n==0 | |||
h = 0; | |||
else | |||
h = 2/T; | |||
end | |||
sum = sum+h*sin(2*pi*n*t/T); | |||
end | |||
plot(t,sum) | |||
title('Quadrature Sampling Waveform') | |||
xlabel('time(T)') | |||
ylabel('Sampling Waveform') | |||
</pre><br> | |||
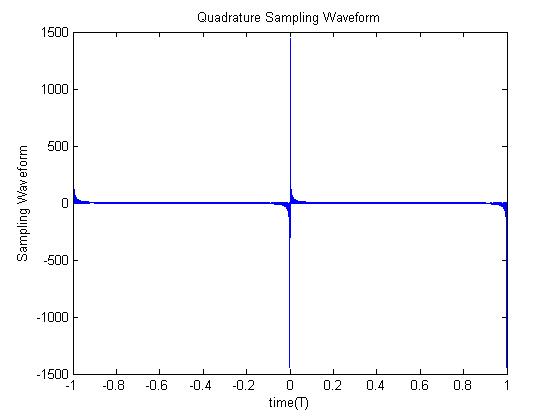
Running the MATLAB script above gives us the following plot.<br> | |||
[[Image:Quadrature sampling.jpg]]<br> | |||
Summing over a smaller range of <math> n \!</math> would look like the following.<br> | |||
<pre> | |||
clear all; | |||
close all; | |||
sum = 0; | |||
T = 1; | |||
t = -T:0.001:T; | |||
N = 100; | |||
for n = 1:N; | |||
if n==0 | |||
h = 0; | |||
else | |||
h = 2/T; | |||
end | |||
sum = sum+h*sin(2*pi*n*t/T); | |||
end | |||
plot(t,sum) | |||
title('Quadrature Sampling Waveform') | |||
xlabel('time(T)') | |||
ylabel('Sampling Waveform') | |||
</pre><br> | |||
[[Image:Quadrature sampling2.jpg]] | |||
Latest revision as of 22:31, 1 December 2009
Max Woesner
Homework #10 - Quadrature sampling waveform plot
Problem Statement
Plot
Solution
While we can't sum to infinity in the computer, we can get a close approximation summing over a large enough range of
I found summing over was about the most the computer could handle reasonably.
The following script was written in MATLAB to produce the desired plot.
clear all;
close all;
sum = 0;
T = 1;
t = -T:0.0001:T;
N = 1000;
for n = 1:N;
if n==0
h = 0;
else
h = 2/T;
end
sum = sum+h*sin(2*pi*n*t/T);
end
plot(t,sum)
title('Quadrature Sampling Waveform')
xlabel('time(T)')
ylabel('Sampling Waveform')
Running the MATLAB script above gives us the following plot.
Summing over a smaller range of would look like the following.
clear all;
close all;
sum = 0;
T = 1;
t = -T:0.001:T;
N = 100;
for n = 1:N;
if n==0
h = 0;
else
h = 2/T;
end
sum = sum+h*sin(2*pi*n*t/T);
end
plot(t,sum)
title('Quadrature Sampling Waveform')
xlabel('time(T)')
ylabel('Sampling Waveform')