Coupled Oscillator: horizontal Mass-Spring: Difference between revisions
| (25 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=Problem Statement= | |||
'''Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes of the system.''' | '''Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes and eigenvectors of the system.''' | ||
[[Image:horizontal spring.jpg]] | [[Image:horizontal spring.jpg]] | ||
| Line 39: | Line 39: | ||
:<math>\dot{x_2}=\dot{x_2}</math> | :<math>\dot{x_2}=\dot{x_2}</math> | ||
==State Equations== | |||
<math> | <math> | ||
| Line 112: | Line 112: | ||
</math> | </math> | ||
== Eigen Values == | |||
'''Once you have your equations of equilibrium in matrix form you can plug them into MATLAB which will give you the eigen values automatically.''' | |||
:'''Given''' | |||
:<math>m_1=10kg\,</math> | |||
:<math>m_2=10kg\,</math> | |||
:<math>k_1=25\,{N\over {m}}</math> | |||
:<math>k_2=50\,{N\over {m}}</math> | |||
'''We now have''' | |||
:<math>\begin{bmatrix} | |||
\dot{x_1} \\ | |||
\ddot{x_1} \\ | |||
\dot{x_2} \\ | |||
\ddot{x_2} | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
0 & 1 & 0 & 0 \\ | |||
-5 & 0 & -2.5 & 0 \\ | |||
0 & 0 & 0 & 1 \\ | |||
2.5 & 0 & 10 & 0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
{x_1} \\ | |||
\dot{x_1} \\ | |||
{x_2} \\ | |||
\dot{x_2} | |||
\end{bmatrix} | |||
+ | |||
\begin{bmatrix} | |||
0 \\ | |||
0 \\ | |||
0 \\ | |||
0 | |||
\end{bmatrix}</math> | |||
'''From this we get''' | |||
:<math>\lambda_1=-3.0937,</math> | |||
:<math>\lambda_2=2.1380i,</math> | |||
:<math>\lambda_3=- 2.1380i,</math> | |||
:<math>\lambda_4=3.0937,</math> | |||
== Eigen Vectors == | |||
'''Using the equation above and the same given conditions we can plug everything into MATLAB and get the eigen vectors which we will denote as <math>k_1,k_2,k_3,k_4\,</math>.''' | |||
:<math>k_1=\begin{bmatrix} | |||
0.0520 \\ | |||
-0.1609 \\ | |||
-0.3031 \\ | |||
0.9378 | |||
\end{bmatrix}</math> | |||
:<math>k_2=\begin{bmatrix} | |||
0.4176i \\ | |||
-0.8928 \\ | |||
- 0.0716i \\ | |||
0.1532 | |||
\end{bmatrix}</math> | |||
:<math>k_3=\begin{bmatrix} | |||
- 0.4176i \\ | |||
-0.8928 \\ | |||
0.0716i \\ | |||
0.1532 | |||
\end{bmatrix}</math> | |||
:<math>k_4=\begin{bmatrix} | |||
-0.0520 \\ | |||
-0.1609 \\ | |||
0.3031 \\ | |||
0.9378 | |||
\end{bmatrix}</math> | |||
==So then the answer is...== | |||
'''We can now plug these eigen vectors and eigen values into the standard equation''' | |||
:<math>x=c_1k_1e^{\lambda_1 t}+c_2k_2e^{\lambda_2 t}+c_3k_3e^{\lambda_3 t}+c_4k_4e^{\lambda_4 t}</math> | |||
<math>\ x=c_1</math><math>\begin{bmatrix}0.0520 \\-0.1609 \\-0.3031\\0.9378\end{bmatrix}\,</math><math>e^{-3.0937}+ c_2</math><math>\begin{bmatrix}0.4176i \\-0.8928\\- 0.0716i\\0.1532\end{bmatrix}\,</math><math>e^{2.1380i}+ c_3</math><math>\begin{bmatrix}- 0.4176i \\-0.8928\\0.0716i\\0.1532\end{bmatrix}\,</math><math>e^{- 2.1380i}+ c_4</math><math>\begin{bmatrix}-0.0520 \\-0.1609\\0.3031\\0.9378\end{bmatrix}\, | |||
</math><math>e^{3.0937}\,</math> | |||
== Matrix Exponential == | |||
'''We now use matrix exponentials to solve the same problem.''' | |||
:<math>z=Tx\,</math> | |||
'''So from the above equation we get this to prove the matrix exponetial works.''' | |||
:<math>\dot{z}=TAT^{-1}z</math> | |||
'''We also know what T equals and we can solve it for our case''' | |||
:<math>T^{-1}=[k_1|k_2|k_3|k_4]\,</math> | |||
:<math>T^{-1}=\begin{bmatrix} | |||
0.0520 & 0.4176i & - 0.4176i & -0.0520 \\ | |||
-0.1609 & -0.8928 & -0.8928 & -0.1609 \\ | |||
-0.3031 & - 0.0716i & 0.0716i & 0.3031 \\ | |||
0.9378 & 0.1532 & 0.1532 & 0.9378 | |||
\end{bmatrix}</math> | |||
'''Taking the inverse of this we can solve for T''' | |||
:<math>T=\begin{bmatrix} | |||
-0.2914 & 0.0943 & -1.6996 & 0.5493 \\ | |||
- 1.2337i & -0.5770 & - 0.2117i & -0.0990 \\ | |||
1.2335i & -0.5770 & 0.2116i & -0.0990 \\ | |||
0.2914 & 0.0943 & 1.6996 & 0.5493 | |||
\end{bmatrix}</math> | |||
'''So taking''' | |||
:<math>\dot{z}=TAT^{-1}z</math> | |||
'''We get the uncoupled matrix of''' | |||
:<math>\dot{z}=\begin{bmatrix} | |||
-3.0937 & 0 & 0 & 0 \\ | |||
0 & 2.1380i & 0 & 0 \\ | |||
0 & 0 & - 2.1380i & 0 \\ | |||
0 & 0 & 0 & 3.0937 | |||
\end{bmatrix}</math> | |||
created by Greg Peterson | |||
Latest revision as of 12:55, 14 December 2009
Problem Statement
Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes and eigenvectors of the system.
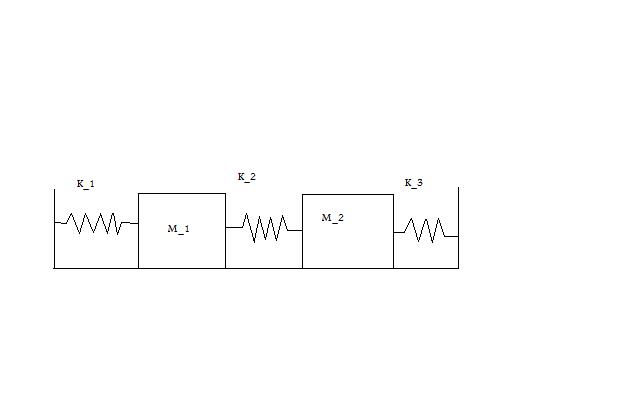
Initial Conditions:
Equations for M_1
Equations for M_2
Additional Equations
State Equations
=
With the numbers...
=
Eigen Values
Once you have your equations of equilibrium in matrix form you can plug them into MATLAB which will give you the eigen values automatically.
- Given
We now have
From this we get
Eigen Vectors
Using the equation above and the same given conditions we can plug everything into MATLAB and get the eigen vectors which we will denote as .
So then the answer is...
We can now plug these eigen vectors and eigen values into the standard equation
Matrix Exponential
We now use matrix exponentials to solve the same problem.
So from the above equation we get this to prove the matrix exponetial works.
We also know what T equals and we can solve it for our case
Taking the inverse of this we can solve for T
So taking
We get the uncoupled matrix of
created by Greg Peterson