Example Problem - Toroid: Difference between revisions
No edit summary |
No edit summary |
||
| (9 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
By: Kirk Betz | |||
'''Problem:''' | '''Problem:''' | ||
Concerning Ampere's law | |||
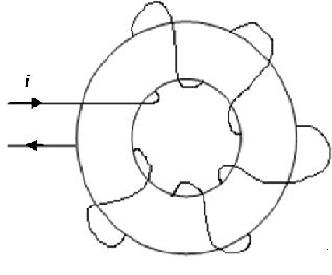
Let look at a coil around a toroid shown in the figure below. The coil has N = 20 turns around the toroid. The toroid has an inside diameter of ID = 4 cm and an outside diameter OD = 5 cm. Determine the field intensity H along the mean path length within the toroid with a current i = 2.5 A. | Let look at a coil around a toroid shown in the figure below. The coil has N = 20 turns around the toroid. The toroid has an inside diameter of ID = 4 cm and an outside diameter OD = 5 cm. Determine the field intensity H along the mean path length within the toroid with a current i = 2.5 A. | ||
[[Image:toroid.jpg]] | [[Image:toroid.jpg]] | ||
''Figure created by Kirk Betz'' | |||
'''Solution:''' | '''Solution:''' | ||
Do symmetry the magnetic field intensity Hm along a circular contour within the toroid is constant. We can find the radius by | Do symmetry the magnetic field intensity Hm along a circular contour within the toroid is constant. We can find the mean radius by | ||
<math>r_m=(\frac{1}{2})\frac{OD + ID}{2} = 2.25\ cm</math> | |||
<math> | Using the mean radius the mean path of length <math>l_m</math> can be calculated. | ||
<math> l_m = { 2 \pi r_m} = 0.141\ </math> | <math> l_m = { 2 \pi r_m} = 0.141\ </math> | ||
With Ampere's Law (below) the field intensity along the mean path can be Found. | |||
<math>H_m=(\frac{Ni}{l_m})</math> | <math>H_m=(\frac{Ni}{l_m})</math> | ||
Finally teh H_m can be calculated. | |||
<math>H_m=\frac{20 x 2.5}{.141}= 354.6\ A /m)</math> | <math>H_m=\frac{20 x 2.5}{.141}= 354.6\ A /m)</math> | ||
Since the width of the toroid is much smaller than the mean radius <math>r_m</math> we can assume a uniform <math>H_m</math> throughout teh cross-section of the toroid. | |||
== Reviewed by == | |||
[[Will Griffith]] | |||
[[Matthew Fetke]] | |||
== Read by == | |||
== Points for page == | |||
Worth 117 | |||
Kirk total for paper 117 + 50 conference = 167 | |||
Latest revision as of 15:41, 20 January 2010
By: Kirk Betz
Problem: Concerning Ampere's law Let look at a coil around a toroid shown in the figure below. The coil has N = 20 turns around the toroid. The toroid has an inside diameter of ID = 4 cm and an outside diameter OD = 5 cm. Determine the field intensity H along the mean path length within the toroid with a current i = 2.5 A.
Figure created by Kirk Betz
Solution:
Do symmetry the magnetic field intensity Hm along a circular contour within the toroid is constant. We can find the mean radius by
Using the mean radius the mean path of length can be calculated.
With Ampere's Law (below) the field intensity along the mean path can be Found.
Finally teh H_m can be calculated.
Since the width of the toroid is much smaller than the mean radius we can assume a uniform throughout teh cross-section of the toroid.
Reviewed by
Read by
Points for page
Worth 117
Kirk total for paper 117 + 50 conference = 167