Alex's Assignment: Difference between revisions
Created page with 'AH HA HA HA HA! RABBIT RABBIT!!!!' |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Alex's Fourier Project== | |||
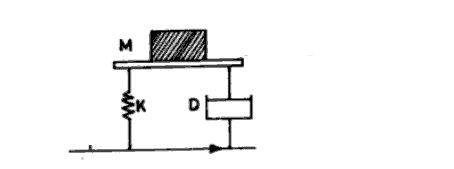
I chose to do my LNA project on a spring mass and dampener system such as what you would find on an automobile. As shown on the picture we have a mass (M), spring (K), and dampener (D). | |||
[[Image:LNAHW-8.jpg|thumb|500px|right]] | |||
==General Equations== | |||
The first thing I need to do is write down the general equations for the Fourier Series: | |||
<math>\begin{align} | |||
x(t) &= x(t+T) = a_0 + \sum_{n=1}^\infty a_n \cos(n\omega_0t) + b_n \sin(n\omega_0t)\\ | |||
\omega_0 &= 2\pi f_0\\ | |||
a_0 &= \frac{1}{T}\int_0^T f(t)\, dt\\ | |||
a_n &= \frac{2}{T}\int_0^T f(t)\cos(n\omega_0t)\, dt\\ | |||
b_n &= \frac{2}{T}\int_0^T f(t)\sin(n\omega_0t)\, dt\\ | |||
\end{align} | |||
</math> | |||
If odd function, <math>a_n = 0</math> | |||
If even function, <math>b_n = 0</math> | |||
==Equations== | |||
Now that we have the basic equations for a Fourier Series we can begin to calculate for the spring dampener system. | |||
knowing that as the vehicle travels down a rough road it creates a displacement x we can equate the formula for the system. | |||
The forces apposing the displacement are: | |||
The mass of the vehicle for one tire <math>\frac{1}{4}M</math> | |||
The spring constant <math>Kx</math> | |||
And the Dampening of the shock <math>Du</math> | |||
Plugging in the forces into an Ordinary Differential Equation we get: | |||
<math>Mu'+Du+Kx=0</math> | |||
Latest revision as of 20:30, 1 November 2010
Alex's Fourier Project
I chose to do my LNA project on a spring mass and dampener system such as what you would find on an automobile. As shown on the picture we have a mass (M), spring (K), and dampener (D).
General Equations
The first thing I need to do is write down the general equations for the Fourier Series:
If odd function,
If even function,
Equations
Now that we have the basic equations for a Fourier Series we can begin to calculate for the spring dampener system. knowing that as the vehicle travels down a rough road it creates a displacement x we can equate the formula for the system. The forces apposing the displacement are:
The mass of the vehicle for one tire
The spring constant
And the Dampening of the shock
Plugging in the forces into an Ordinary Differential Equation we get: