Matthew's Asgn: Difference between revisions
Btheredude (talk | contribs) No edit summary |
Btheredude (talk | contribs) No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 24: | Line 24: | ||
Therefore the Resulting Equation for the system after applying the Laplace Transform: | Therefore the Resulting Equation for the system after applying the Laplace Transform: | ||
<math>\ 0 = -s | <math>\ 0 = \dfrac{-s}{(s^2+w^2)} + RI(s) + LsI(s) - Li \,\!</math> | ||
A series of algebraic manipulations follows to come up with I(s): | A series of algebraic manipulations follows to come up with I(s): | ||
| Line 36: | Line 36: | ||
We can then use partial fraction manipulation to expand the expression: | We can then use partial fraction manipulation to expand the expression: | ||
<math>\ s | <math>\ \dfrac{s}{(s^2+w^2)(R+Ls)} = \dfrac{A}{(s+jw)} + \dfrac{A*}{(s-jw)} + \dfrac{B}{(Ls+R)} \,\!</math> | ||
<math>\ | <math>\ \dfrac{s/L}{(s^2+w^2)(R/L+s)} = \dfrac{A(s+jw)(s+R/L)}{(s+R/L)(s^2+w^2)} + \dfrac{A*(s+jw)(s+R/L)}{(s^2+w^2)(s+R/L)} + \dfrac{B(s^2+w^2)}{(s+R/L)(s^2+w^2)} \,\!</math> | ||
<math> \dfrac{S}{L} = A(s-jw)(s+R/L) + A*((s+jw)(s+R/L)) + B(s^2+w^2) \,\!</math> | |||
<math> \dfrac{S}{L} = A(s^2-jws+R/Ls-jwR/L) + A*(s^2+jws+R/L+jwr/L) + B(s^2+w^2) \,\!</math> | |||
<math> \dfrac{S}{L} = s^2(A+A*+B) + s((A*-A)jws+(A*+A)R/L) + (A*-A)Rjw/L+Bw^2 \,\!</math> | |||
After a lot of messy math and work: | |||
<math> A = \dfrac{1/2}{R-jwL} \,\!</math> | |||
<math> A* = \dfrac{1/2}{R+jwL} \,\!</math> | |||
<math> B = \dfrac{-R}{R^2+w^2L^2} \,\!</math> | |||
<math> I(s)= \dfrac{a+jb}{s+jw} + \dfrac{a-jb}{s-jw} + \dfrac{B}{s+R/L} \,\!</math> | |||
<math> I(s)= \dfrac{(a+jb)(s-jw)+(a-jb)(s+jw)}{s^2+w^2}+\dfrac{B}{s^2+w^2} \,\!</math> | |||
<math> I(s)= \dfrac{2as}{s^2+w^2} + \dfrac{2bw}{s^2+w^2} + \dfrac{B}{s+R/L} \,\!</math> | |||
<math> a = \dfrac{1/2R}{R^2+w^2L^2} \,\!</math> | |||
<math> b = \dfrac{1/2wL}{R^2+w^2L^2} \,\!</math> | |||
<math> i(t) = \mathcal{L}^{-1} \{I(s)\} \,\!</math> | |||
<math> i(t) = 2a \cos wt + 2b\sin wt + BE^{-Rt/L} -ie^{-Rt/L} \,\!</math> | |||
<math> i(t) = 2 \dfrac{R}{R^2+w^2L^2} \cos wt + 2 \dfrac{wL}{R^2+w^2L^2} \sin wt + \dfrac{-R}{R^2+w^2L^2} e^{-Rt/L} -ie^{-Rt/L} \,\!</math> | |||
This Solves the Series RL circuit for the current throughout the circuit, given initial conditions or no initial conditions | |||
Latest revision as of 17:40, 1 November 2010
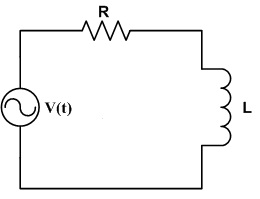
I decided that I would attempt to perform a simple analysis of a series RL circuit, which could then be used to do a more complex analysis on a basic transformer. I have always had interest in electronics, and transformers are key to basic electronics.
I decided that i would do the analysis of a RL circuit with the variables instead of given values.
Given:
V(t)=
V(s)=
I(0)=i
The Laplace transform for an inductor:
=
The Laplace transform for a resistor:
=
Therefore the Resulting Equation for the system after applying the Laplace Transform:
A series of algebraic manipulations follows to come up with I(s):
We can then use partial fraction manipulation to expand the expression:
After a lot of messy math and work:
This Solves the Series RL circuit for the current throughout the circuit, given initial conditions or no initial conditions