Magnetic Flux

Magnetic Flux

By: Jason Osborne

Reviewed By: Will Griffith & Wesley Brown

Magnetic Flux is the measure of the strength of a magnetic field over a given area. <ref>http://www.google.com/search?hl=en&safe=off&client=firefox-a&rls=org.mozilla:en-US:official&hs=lBE&defl=en&q=define:magnetic+flux&ei=gsNKS7r4EYuqsgPdmMT_Bg&sa=X&oi=glossary_definition&ct=title&ved=0CAcQkAE</ref>The Greek letter used to represent flux is Φ, phi. The SI unit for magnetic flux is the Weber. The area used must be perpendicular to the

travel of

Figure 1: Magnetic Flux

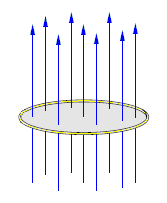
the magnetic lines. The flux can then be determined by how many magnetic lines go

through the area surface. The net flux is the number of magnetic lines going through the area surface in one direction minus the number magnetic lines going through the surface area in the opposite direction. The general quantitative expression for finding magnetic flux is:

$\Phi _{m}=\int \!\!\!\!\int _{S}\mathbf {B} \cdot d\mathbf {A}$

where

B is the magnetic field

A is the surface area<ref>http://en.wikipedia.org/wiki/Magnetic_flux</ref>

If specific situations arise and more variables are known the calculations for magnetic flux can become relatively simple. There are many ways to determine magnetic flux from a variety of equations.

Using Voltage, Time, and Turns of wire

$\Phi _{m}=V\cdot T/overN$

where

V= Voltage

T= Time

N= Number of Turns of wire used

Using Magnetomotive force and the Reluctance

$\Phi _{m}=\mathbf {F_{m}} /\mathbf {R_{m}}$

where

F_m= Magnetomotive Force

R_m= Reluctance

Using Ohm's Law

$\Phi _{m}=\mathbf {I} \cdot \mathbf {L} /\mathbf {N}$

where

I= Current

L= Inductance

N= Number of Turns of wire used<ref>http://info.ee.surrey.ac.uk/Workshop/advice/coils/terms.html</ref>

Using Area and Magnetic Flux Density

$\Phi _{m}=\mathbf {A} \cdot \mathbf {B_{m}}$ where

A= Area of surface where density is measured

B_m=Magnetic Flux Density<ref>Electric Drives an Integrated Approach,Mohan, Ned,2003</ref>

References

<references/>

Readers

Christopher Garrison Lau I