Using the DFT: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 10: | Line 10: | ||
clear all; | clear all; | ||
t=0:.01:2; | t=0:.01:2; | ||
T=1/3; | T=1/3; | ||
ts=0:T:2; | ts=0:T:2; | ||
f1=2; | f1=2; | ||
f2=1/0.125; | f2=1/0.125; | ||
x = sin(2*pi*ts); %this is the function | x = sin(2*pi*ts); %this is the function | ||
plot(ts,sin(2*pi*ts),'r-',t,sin(2*pi*t)); % plot the original signal and the signal sampled at 3Hz | plot(ts,sin(2*pi*ts),'r-',t,sin(2*pi*t)); % plot the original signal and the signal sampled at 3Hz | ||
X = fft(x); % take the DFT | X = fft(x); % take the DFT | ||
pause (2); | pause (2); | ||
plot (ts,X); %plot the DFT of the signal sampled at 3Hz | plot (ts,X); %plot the DFT of the signal sampled at 3Hz | ||
pause (4); | pause (4); | ||
x=sin(2*pi*t); | x=sin(2*pi*t); | ||
plot(t,x); | plot(t,x); | ||
pause(2); | pause(2); | ||
X = fft(x); | X = fft(x); | ||
plot(t,X); %plot the DFT of the original signal | plot(t,X); %plot the DFT of the original signal | ||
Revision as of 10:11, 27 November 2007
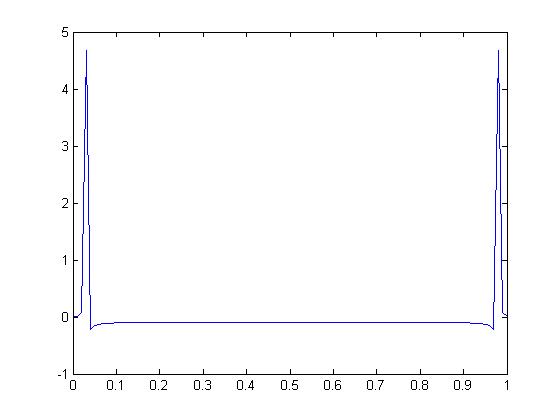
sampling and taking the DFT we get this graph:
Script for matlab:
clear all;
t=0:.01:2;
T=1/3;
ts=0:T:2;
f1=2;
f2=1/0.125;
x = sin(2*pi*ts); %this is the function
plot(ts,sin(2*pi*ts),'r-',t,sin(2*pi*t)); % plot the original signal and the signal sampled at 3Hz
X = fft(x); % take the DFT
pause (2);
plot (ts,X); %plot the DFT of the signal sampled at 3Hz
pause (4);
x=sin(2*pi*t);
plot(t,x);
pause(2);
X = fft(x);
plot(t,X); %plot the DFT of the original signal