Using the DFT: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
This is what we get when we sample the signal at 3Hz | This is what we get when we sample the signal at 3Hz | ||
[[Image:hw13_1.jpg]] | [[Image:hw13_1.jpg]] | ||
Taking the original signal <math>sin(2*pi*t)</math> and applying the DFT we get this graph: | Taking the original signal <math>sin(2*pi*t)</math> and applying the DFT we get this graph: | ||
[[Image:Signals-13.jpg]] | [[Image:Signals-13.jpg]] | ||
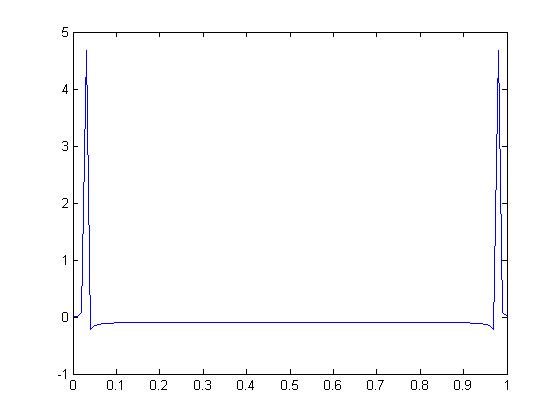
Now taking the DFT of this sampled signal, we get a graph like this: | Now taking the DFT of this sampled signal, we get a graph like this: | ||
[[Image:hw13_2.jpg]] | [[Image:hw13_2.jpg]] | ||
Latest revision as of 10:18, 27 November 2007
This is what we get when we sample the signal at 3Hz
Taking the original signal and applying the DFT we get this graph:
Now taking the DFT of this sampled signal, we get a graph like this:
Script for matlab:
clear all;
t=0:.01:2;
T=1/3;
ts=0:T:2;
f1=2;
f2=1/0.125;
x = sin(2*pi*ts); %this is the function
plot(ts,sin(2*pi*ts),'r-',t,sin(2*pi*t)); % plot the original signal and the signal sampled at 3Hz
X = fft(x); % take the DFT
pause (2);
plot (ts,X); %plot the DFT of the signal sampled at 3Hz
pause (4);
x=sin(2*pi*t);
plot(t,x);
pause(2);
X = fft(x);
plot(t,X); %plot the DFT of the original signal