Laplace transforms: Critically Damped Spring Mass system: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
|||
| Line 118: | Line 118: | ||
Find the Break points using the transfer function | Find the Break points using the transfer function | ||
==Transfer fucntion== | ===Transfer fucntion=== | ||
<math>\mathbf {X}(s)=-\frac{4}{(s+2)^2} </math><br /><br /> | <math>\mathbf {X}(s)=-\frac{4}{(s+2)^2} </math><br /><br /> | ||
Revision as of 14:57, 27 October 2009
Using the Laplace Transform to solve a spring mass system that is critically damped
Problem Statement
An 98 Newton weight is attached to a spring with a spring constant k of 40 N/m. The spring is stretched 4 m and rests at its equilibrium position. It is then released from rest with an initial upward velocity of 2 m/s. The system contains a damping force of 40 times the initial velocity.
Solution
Given
Solving the problem
Apply the Initial and Final Value Theorems to find the initial and final values
- Initial Value Theorem
- Final Value Theorem
Applying this to our problem
Bode Plot of the transfer function
Transfer Function
Bode Plot
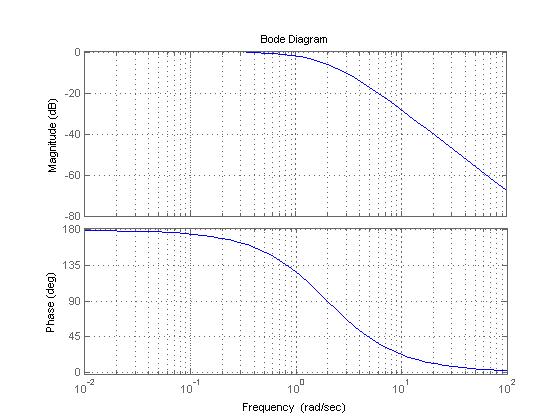
Break Points
Find the Break points using the transfer function
Transfer fucntion
Created by Greg Peterson
Checked by Mark Bernet