8 - 1x oversampling: Difference between revisions
New page: Write a section on the Wiki about how a CD player works with no oversampling, but digital filtering (1x oversampling)<br><br> First we sample the data at <math> f_s = \frac{1}{T} </math> ... |
No edit summary |
||
| Line 12: | Line 12: | ||
and <math> \frac{1}{T}\sum_{n=-\infty}^\infty X(f - \frac{n}{T})</math> in the frequency domain. <br><br> | and <math> \frac{1}{T}\sum_{n=-\infty}^\infty X(f - \frac{n}{T})</math> in the frequency domain. <br><br> | ||
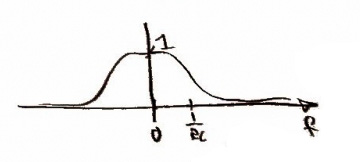
Now that we have the data in the computer we want to convolve it with another impulse function <math> \sum_{m=-M}^M h(\frac{mT}{n})\delta(t-\frac{mT}{n})</math> in the time domain. This is where more that 1x oversampling would occur replace n for nx oversampling, but in our case we use n = 1. Doing this convolution we can also shape our frequency when you convolve in time it multiplies in frequency. So we pick a frequency function <math> \sum_{m=-M}^M h(\frac{mT}{n})e^{-j2\pi fm\frac{T}{n}} </math> to multiply by so our frequency won't overlap later and help compensate for losses in the D/A converter. | Now that we have the data in the computer we want to convolve it with another impulse function <math> \sum_{m=-M}^M h(\frac{mT}{n})\delta(t-\frac{mT}{n})</math> in the time domain. This is where more that 1x oversampling would occur replace n for nx oversampling, but in our case we use n = 1. Doing this convolution we can also shape our frequency when you convolve in time it multiplies in frequency. So we pick a frequency function <math> \sum_{m=-M}^M h(\frac{mT}{n})e^{-j2\pi fm\frac{T}{n}} </math> to multiply by so our frequency won't overlap later and help compensate for losses in the D/A converter. Example the frequency function is. <br><br> | ||
<math> \sum_{m=-M}^M h(\frac{mT}{n})e^{-j2\pi fm\frac{T}{n}} \Longrightarrow </math> [[Image:x_frequency3a.jpg]]<br> | |||
Now doing the convolution/multiplication yields. <br> | |||
The time domain stays the same with [[Image:x_discrete_a.jpg]]<br> | |||
But frequency <br> [[Image:x_frequency2a.jpg|thumb|none|upright = 1|]]x[[Image:x_frequency3a.jpg|thumb|none|upright = 1|]]=[[Image:x_frequency4a.jpg|thumb|none|upright = 1|]]<br><br> | |||
[[Image:x_frequency3a.jpg]]<br> | [[Image:x_frequency3a.jpg]]<br> | ||
Revision as of 17:51, 8 November 2009
Write a section on the Wiki about how a CD player works with no oversampling, but digital filtering (1x oversampling)
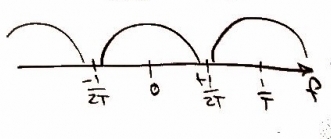
First we sample the data at to get the data in digital form and when you use the impulse function in time the frequency repeats forever as shown
Sample
Where the impulse function with respect to time =
and in the frequency domain.
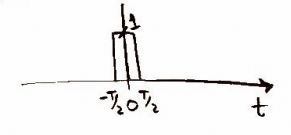
Now that we have the data in the computer we want to convolve it with another impulse function in the time domain. This is where more that 1x oversampling would occur replace n for nx oversampling, but in our case we use n = 1. Doing this convolution we can also shape our frequency when you convolve in time it multiplies in frequency. So we pick a frequency function to multiply by so our frequency won't overlap later and help compensate for losses in the D/A converter. Example the frequency function is.

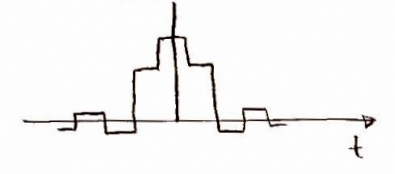
Now doing the convolution/multiplication yields.
The time domain stays the same with 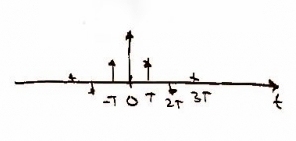
But frequency
x
=