LNA: Difference between revisions
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
[[Image:Circuitben.jpg]] | [[Image:Circuitben.jpg]] | ||
---- | |||
=====Write Each Components in Laplace Form===== | |||
Go from the "t" to the "s" domain right off the bat. Using KVL and assuming the current from ground through the voltage source>resister>capacitor>back to ground. | |||
Voltage Source in Volts: <math>v(t)</math> -> - | Voltage Source in Volts: <math>v(t)</math> -> - | ||
| Line 16: | Line 18: | ||
Resister in OHMs: r -> R | Resister in OHMs: r -> R | ||
Capacitor in Farads: c -> 1/( | Capacitor in Farads: c -> 1/(CS) - <math>V_c</math>(0) Where <math>V_c</math> is the initial voltage of the cap. | ||
===== | |||
-<math> | ---- | ||
=====Apply KVL to Circuit B in S Domain===== | |||
-<math>\tfrac{V_t(0)}{S}</math>+I(s)(R+<math>\tfrac{1}{CS}</math>)-<math>V_c</math>(0)=0 | |||
---- | |||
=====Solving for I(S)===== | =====Solving for I(S)===== | ||
<math>I(S)=\cfrac{V_t(0)+V_c(0)}{S(R+\tfrac{1}{CS})}=\cfrac{(V_t(0)+V_c(0))}{SR+\tfrac{1}{C}}\frac{\tfrac{1}{R}}{\tfrac{1}{R}}=\cfrac{\tfrac{V_t(0)+V_c(0)}{R}}{S+\tfrac{1}{RC}} | <math>I(S)=\cfrac{V_t(0)+V_c(0)}{S(R+\tfrac{1}{CS})}=\cfrac{(V_t(0)+V_c(0))}{SR+\tfrac{1}{C}}\frac{\tfrac{1}{R}}{\tfrac{1}{R}}=\cfrac{\tfrac{V_t(0)+V_c(0)}{R}}{S+\tfrac{1}{RC}} | ||
| Line 24: | Line 30: | ||
</math> | </math> | ||
---- | |||
=====Performing the inverse Laplace===== | =====Performing the inverse Laplace===== | ||
<math> | <math> | ||
L^{-1}(I(S))=L^{-1}(\cfrac{\tfrac{V_t(0)+V_c(0)}{R}}{S+\tfrac{1}{RC}})=i(t)=\frac{V_t(0)+V_c(0)}{ | L^{-1}(I(S))=L^{-1}(\cfrac{\tfrac{V_t(0)+V_c(0)}{R}}{S+\tfrac{1}{RC}})=i(t)=\frac{V_t(0)+V_c(0)}{r}e^{(-\tfrac{1}{rC}t)} | ||
</math> | |||
---- | |||
=====Apply Initial Conditions===== | |||
<math>V_t(0) = 7v</math> | |||
<math>r = 40 Ω</math> | |||
<math>c = 2 F</math> | |||
<math>V_c(0) = 3v</math> | |||
<math> | |||
i(t)=\frac{V_t(0)+V_c(0)}{r}e^{(-\tfrac{1}{rC}t)}=\frac{7+3}{40}e^{(-\tfrac{1}{40*2}t)}=\tfrac{1}{4}e^{-\tfrac{1}{40}t} | |||
</math> | </math> | ||
Revision as of 10:21, 10 November 2009
Ben Henry LNA Homework
HW#5
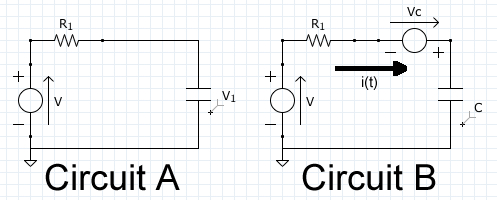
The below problem, although simple, is done with variables so that values can be plugged in afterwords. Thus one can see how the problem progresses and see where the initial conditions end up at the end. PROBLEM STATEMENT: Solve for current i(t) in CIRCUIT A below using Laplace Transforms. The two circuits (A and B below) are the same circuit. B is the same as A, only it shows are current when we use KVL and after we have moved the circuit into the "S" domain.
Write Each Components in Laplace Form
Go from the "t" to the "s" domain right off the bat. Using KVL and assuming the current from ground through the voltage source>resister>capacitor>back to ground.
Voltage Source in Volts: -> - (0)/S
Resister in OHMs: r -> R
Capacitor in Farads: c -> 1/(CS) - (0) Where is the initial voltage of the cap.
Apply KVL to Circuit B in S Domain
-+I(s)(R+)-(0)=0
Solving for I(S)
Performing the inverse Laplace
Apply Initial Conditions
Failed to parse (syntax error): {\displaystyle r = 40 Ω}