HW8: Difference between revisions
New page: '''Problem Statement''' Write a section describing how a CD player works with out oversampling but with digital filtering (1x oversampling) '''Solution''' CD players are used to play au... |
No edit summary |
||
| Line 8: | Line 8: | ||
[[Image:x_continuous3.jpg]] [[Image:x_frequency1b.jpg]]<br> | [[Image:x_continuous3.jpg]] [[Image:x_frequency1b.jpg]]<br> | ||
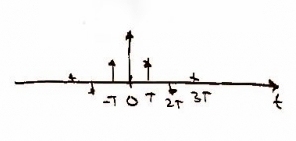
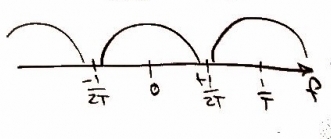
In order to take the signal and read it digitally we must sample it. This gives us data points creating a discrete function of time <math> x(nT)\!</math>, where <math> n\!</math> is and integer and <math> T\!</math> is the period between samples. We use a frequency of 44 kHz as it is twice the frequency at which a human can hear (i.e. 2 x 22 kHz) -- that means, <math>\scriptstyle f_{s} = 44</math> kHz. Mathematically sampling is represented by multiplying x(t) with the delta function which results in a convolution with X(f). | |||
[[Image:x_discrete_a.jpg ]] [[Image:x_frequency2a.jpg]]<br> | |||
Represented as: <math> \sum_{n=-\infty}^{\infty}x(nT) \delta (t-nT_{0})</math> and <math>\frac{1}{T}\sum_{n=-\infty}^{\infty}X(f-\frac{n}{T})</math> respectively. | |||
Revision as of 23:41, 24 November 2009
Problem Statement
Write a section describing how a CD player works with out oversampling but with digital filtering (1x oversampling)
Solution
CD players are used to play audio files and although these are limited we can look at any non periodic signal as periodic with an infinite period. We can represent this signal, x(t) as such in the time domain and X(f) in the frequency domain.
In order to take the signal and read it digitally we must sample it. This gives us data points creating a discrete function of time , where is and integer and is the period between samples. We use a frequency of 44 kHz as it is twice the frequency at which a human can hear (i.e. 2 x 22 kHz) -- that means, kHz. Mathematically sampling is represented by multiplying x(t) with the delta function which results in a convolution with X(f).
Represented as: and respectively.