Coupled Oscillator: Hellie

Problem Statement

Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes of the system.

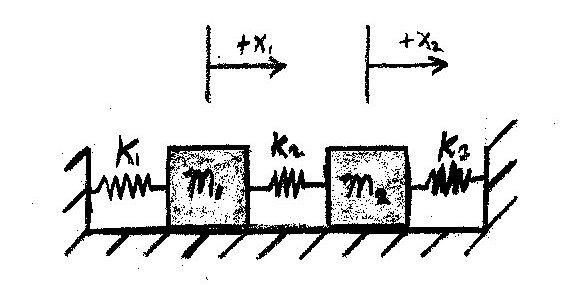
Initial Conditions:

$m_1=15kg$

$m_2=15kg$

$k1=100N/m$

$k2=150N/m$

$k3=100N/m$

State Equations

$\left[\begin{array}{c}\dot{x_1}\\ \ddot{x_1}\\ \dot{x_2}\\ \ddot{x_2}\end{array}\right]$ = $\left[\begin{array}{cccc}0& 1& 0& 0\\ \frac{(k_1-k_2)}{m_1}& 0& \frac{-k_1}{m_1}& 0\\ 0& 0& 0& 1\\ \frac{k_1}{m_2}& 0& \frac{(k_1+k_2)}{m_2}& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ {\dot{x}}_1\\ x_2\\ {\dot{x}}_2\end{array}\right]+\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$

Eigenmodes

There are three eigenmodes for the system

1) m1 and m2 oscillating together

2) m1 and m2 oscillating at exactly a half period difference

3) m1 and m2 oscillating at different times

Solve Using the Matrix Exponential

Written by: Andrew Hellie