Coupled Oscillator: Hellie: Difference between revisions
Jump to navigation
Jump to search
| Line 105: | Line 105: | ||
<math>e^{At}=\mathcal{L}^{-1}\left\{ | <math>e^{At}=\mathcal{L}^{-1}\left\{[SI-A]^{-1}\right\}\,</math> | ||
<math>[SI-A]\,</math> | |||
= | |||
<math> | |||
\begin{bmatrix} | |||
S&1&0&0 \\ | |||
\frac{(-50 N/m)}{15 kg}&S&\frac{-100 N/m}{15 kg}&0 \\ | |||
0&0&S&1 \\ | |||
\frac{100 N/m}{15 kg}&0&\frac{(250 N/m)}{15 kg}&S | |||
\end{bmatrix} | |||
</math> | |||
Written by: Andrew Hellie | Written by: Andrew Hellie | ||
Revision as of 20:05, 30 November 2009
Problem Statement
Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes of the system.
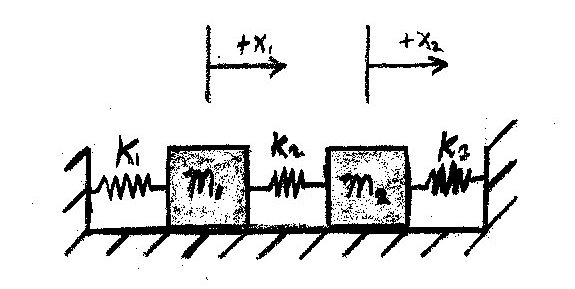
Initial Conditions:
State Equations
=
With the numbers...
=
Eigenmodes
- There are three eigenmodes for the system
- 1) m1 and m2 oscillating together
- 2) m1 and m2 oscillating at exactly a half period difference
Solve Using the Matrix Exponential
=
Written by: Andrew Hellie