Coupled Oscillator: horizontal Mass-Spring

Problem Statement

Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes of the system.

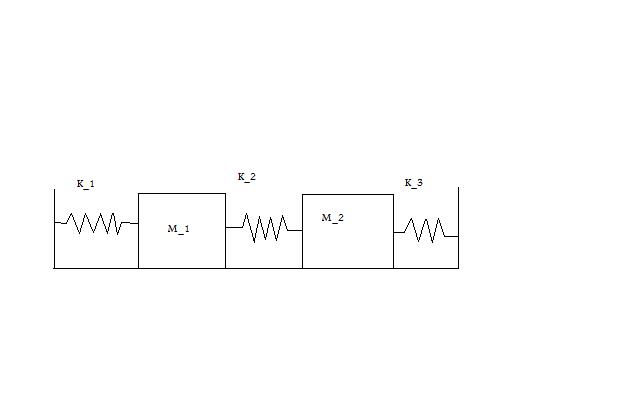
Initial Conditions:

$m_{1}=10kg\,$

$m_{2}=10kg\,$

$k1=25N/m\,$

$k2=75N/m\,$

$k3=50N/m\,$

Equations for M_1

${\begin{alignedat}{3}F&=ma\\F&=m{\ddot {x}}\\-k_{1}x_{1}-k_{2}(x_{1}x_{2})&=m_{1}{\ddot {x_{1}}}\\-{k_{1}x_{1} \over {m_{1}}}-{k_{2}(x_{1}-x_{2}) \over {m_{1}}}&=m_{1}{\ddot {x_{1}}}\\-{k_{1}x_{1} \over {m_{1}}}-{k_{2}(x_{1}-x_{2}) \over {m_{1}}}&={\ddot {x_{1}}}\\-{k_{1}+k_{2} \over {m_{1}}}x_{1}+{k_{2} \over {m_{1}}}x_{2}&={\ddot {x_{1}}}\\\end{alignedat}}$

Equations for M_2

${\begin{alignedat}{3}F&=ma\\F&=m{\ddot {x}}\\-k_{2}(x_{2}-x_{1})&=m_{2}{\ddot {x_{2}}}\\{-k_{2}(x_{2}-x_{1}) \over {m_{2}}}&={\ddot {x_{2}}}\\-{k_{2} \over {m_{2}}}x_{2}+{k_{2} \over {m_{2}}}x_{1}&={\ddot {x_{2}}}\\\end{alignedat}}$

Additional Equations

${\dot {x_{1}}}={\dot {x_{1}}}$

${\dot {x_{2}}}={\dot {x_{2}}}$

State Equations

${\begin{bmatrix}{\dot {x_{1}}}\\{\ddot {x_{1}}}\\{\dot {x_{2}}}\\{\ddot {x_{2}}}\end{bmatrix}}\,$ = ${\begin{bmatrix}0&1&0&0\\{\frac {(k_{1}-k_{2})}{m_{1}}}&0&{\frac {-k_{1}}{m_{1}}}&0\\0&0&0&1\\{\frac {k_{1}}{m_{2}}}&0&{\frac {(k_{1}+k_{2})}{m_{2}}}&0\end{bmatrix}}{\begin{bmatrix}x_{1}\\{\dot {x}}_{1}\\x_{2}\\{\dot {x}}_{2}\end{bmatrix}}+{\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}}{\begin{bmatrix}0\\0\\0\\0\end{bmatrix}}$

With the numbers...

${\begin{bmatrix}{\dot {x_{1}}}\\{\ddot {x_{1}}}\\{\dot {x_{2}}}\\{\ddot {x_{2}}}\end{bmatrix}}\,$ = ${\begin{bmatrix}0&1&0&0\\{\frac {(-50N/m)}{10kg}}&0&{\frac {-25N/m}{10kg}}&0\\0&0&0&1\\{\frac {25N/m}{10kg}}&0&{\frac {(100N/m)}{10kg}}&0\end{bmatrix}}{\begin{bmatrix}x_{1}\\{\dot {x}}_{1}\\x_{2}\\{\dot {x}}_{2}\end{bmatrix}}$