Coupled Oscillator: horizontal Mass-Spring: Difference between revisions
| Line 205: | Line 205: | ||
:<math>T^{-1}=[k_1|k_2|k_3|k_4]\,</math> | :<math>T^{-1}=[k_1|k_2|k_3|k_4]\,</math> | ||
:<math>T^{-1}=\begin{bmatrix} | :<math>T^{-1}=\begin{bmatrix} | ||
0 | 0 & 0 & 0 & 0 \\ | ||
0 & 0 & 0 & 0 \\ | |||
0 & 0 & 0 & 0 \\ | |||
0 | 0 & 0 & 0 & 0 | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
Taking the inverse of this we can solve for T | Taking the inverse of this we can solve for T | ||
:<math>T=\begin{bmatrix} | :<math>T=\begin{bmatrix} | ||
0 & 0 & 0 & 0 \\ | |||
0 & 0 & 0 & 0 \\ | |||
0 | 0 & 0 & 0 & 0 \\ | ||
0 & 0 & 0 & 0 | |||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
Revision as of 13:59, 10 December 2009
Problem Statement
Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes and eigenvectors of the system.
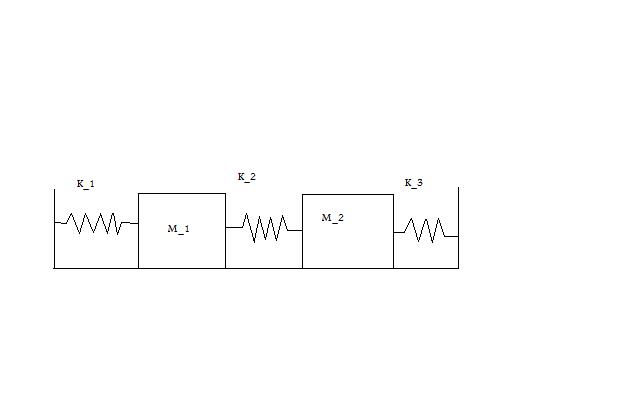
Initial Conditions:
Equations for M_1
Equations for M_2
Additional Equations
State Equations
=
With the numbers...
=
Eigen Values
Once you have your equations of equilibrium in matrix form you can plug them into a calculator or a computer program that will give you the eigen values automatically. This saves you a lot of hand work. Here's what you should come up with for this particular problem given these initial conditions.
- Given
We now have
From this we get
Eigen Vectors
Using the equation above and the same given conditions we can plug everything to a calculator or computer program like MATLAB and get the eigen vectors which we will denote as .
Matrix Exponential
In this section we will use matrix exponentials to solve the same problem. First we start with this identity.
This can be rearranged by multiplying the inverse of T to the left side of the equation.
Now we can use another identity that we already know
Combining the two equations we then get
Multiplying both sides of the equation on the left by T we get
We also know what T equals and we can solve it for our case
Taking the inverse of this we can solve for T