Transformer example problem

Problem:

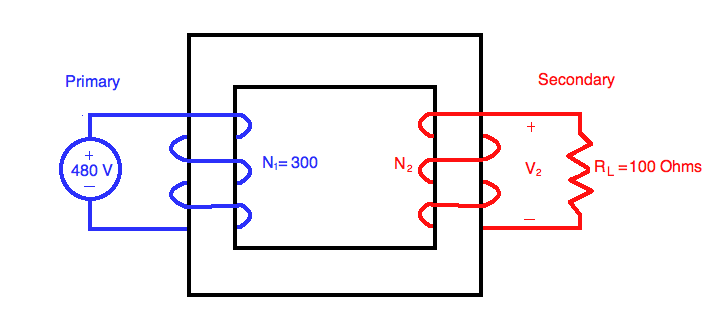
An ideal transformer with a 300 turn primary connected to a 480 V, 60 Hz supply line needs to output 120 V from the secondary. If a 100 Ω resistor is connected across the secondary, determine: A) How many turns the secondary must have to output the desired voltage. B) The current through the resistor, C)The current drawn through the primary. D) The maximum flux in the core of the transformer

Solution:

Part A:

The ratio of primary voltage to secondary voltage is directly proportional to the ratio of number of turns on the primary to number of turns on the secondary:

$\frac{V_1}{V_2}=\frac{N_1}{N_2}$

Where $V_1=$Voltage across primary, $V_2=$Voltage across secondary, $N_1=$ Number of turns in primary, $N_2=$ Number of turns in secondary

$$\begin{gathered} \frac{480 \\ volts}{120 \\ volts}=\frac{300 \\ turns}{N_2} \end{gathered}$$

To solve for the number of turns required for the secondary, the equation is rearranged solving for $N_2=$:

$$\begin{gathered} N_2=\frac{300\cdot 120}{480}\Rightarrow N_2=75 \\ turns \end{gathered}$$

Part B:

The voltage across the secondary is given in the problem statement as 120 volts. Using ohms law, $V=i\cdot R$, we can solve for the current in the loop ($i_2$ ).
$i_2=\frac{V_2}{R_L}$
Where $i_2=$ Current through secondary, $V_2=$Voltage across secondary, $R_L=$ Load Resistor ($R_L=$ 100 Ω)

$$\begin{gathered} i_2=\frac{120 \\ volts}{100 \\ \mathrm{\Omega }}\Rightarrow i_2=1.2 \\ A \end{gathered}$$

Part C:

The ratio of primary current to secondary current is inversely proportional to the ratio of number of turns on the primary to number of turns on the secondary:

$\frac{i_1}{i_2}=\frac{N_2}{N_1}$
Where $i_1=$Current in primary, $i_2=$Current in secondary, $N_1=$ Number of turns in primary, $N_2=$ Number of turns in secondary

$$\begin{gathered} \frac{i_1}{1.2 \\ A}=\frac{75 \\ turns}{300 \\ turns} \end{gathered}$$

Rearranging to solve for $i_1$:

$$\begin{gathered} {i}_1=i_2\cdot \frac{N_2}{N_1}\Rightarrow 1.2A\cdot \frac{75 \\ turns}{300 \\ turns}\Rightarrow i_1=.3 \\ A \end{gathered}$$

Part D:

The induced emf of the secondary can be calculated by: $$\begin{gathered} V_2=4.44 \\ \cdot {f}\cdot N_2\cdot {\mathrm{\Phi }}_m \\ \mathrm{\angle }{0}^{\circ } \end{gathered}$$<ref>Guru and Huseyin, Electric Machinery and Transformers, 3rd ed. (New York: Oxford University Press, 2001), 209.</ref> Solving for ${\mathrm{\Phi }}_m$, we can calculate the maximum flux in the core: ${\mathrm{\Phi }}_m=\frac{V_2}{4.44\cdot {f}\cdot N_2}$

Where $$\begin{gathered} {\mathrm{\Phi }}_m \\ = \end{gathered}$$max flux in core, $V_2=$Voltage across secondary, ${f}=$ Frequency of line, $N_2=$ Number of turns in secondary

$$\begin{gathered} {\mathrm{\Phi }}_m=\frac{120}{4.44\cdot 60 \\ Hz\cdot 75}\Rightarrow {\mathrm{\Phi }}_m=6.006 \\ mWb \end{gathered}$$

References:

<references/>

Authors:

Tim Rasmussen