Fourier Example: Difference between revisions
Jump to navigation
Jump to search
Jorge.cruz (talk | contribs) No edit summary |
Jorge.cruz (talk | contribs) No edit summary |
||
| Line 44: | Line 44: | ||
==Solution Graph== | ==Solution Graph== | ||
[[Image:Fourier.gif]] | [[Image:Fourier.gif]] | ||
==***BONUS*** VIDEO! (For people completely lost on Fourier Series)== | |||
http://www.youtube.com/watch?v=nXEqrOt-nB8 | |||
==References:== | ==References:== | ||
[[Fourier Series: Basic Results]] | [[Fourier Series: Basic Results]] | ||
Revision as of 13:18, 21 January 2010
Find the Fourier Series of the function:
Solution
Here we have
and
We obtain = 0 and
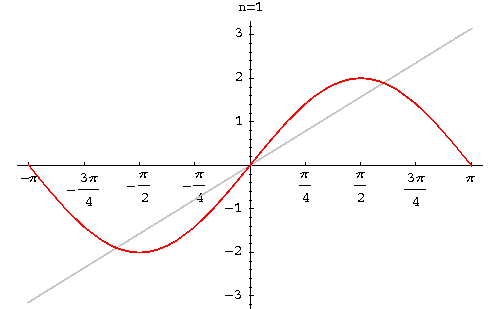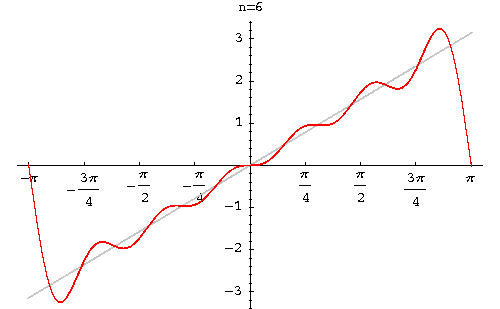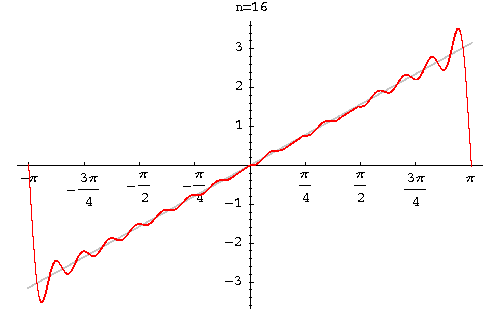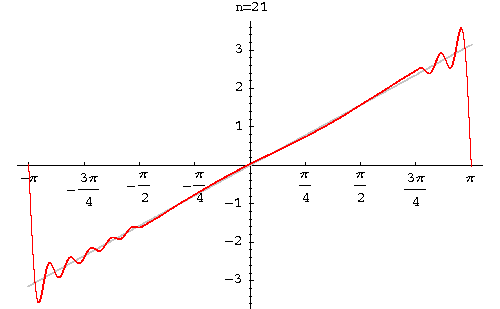
Therefore, the Fourier series of f(x) is
Solution Graph
***BONUS*** VIDEO! (For people completely lost on Fourier Series)
http://www.youtube.com/watch?v=nXEqrOt-nB8