Cascading Scattering Parameters and Calibration of a VNA Using the Short, Open, Load, Through (SLOT) Method

S Parameters of Cascaded Networks

The scattering matrix of cascaded networks can be obtained by adding all the Feynman paths through the networks. Here is a photo from the class notes on finding the overall reflection coefficient of two cascaded scattering matrices. 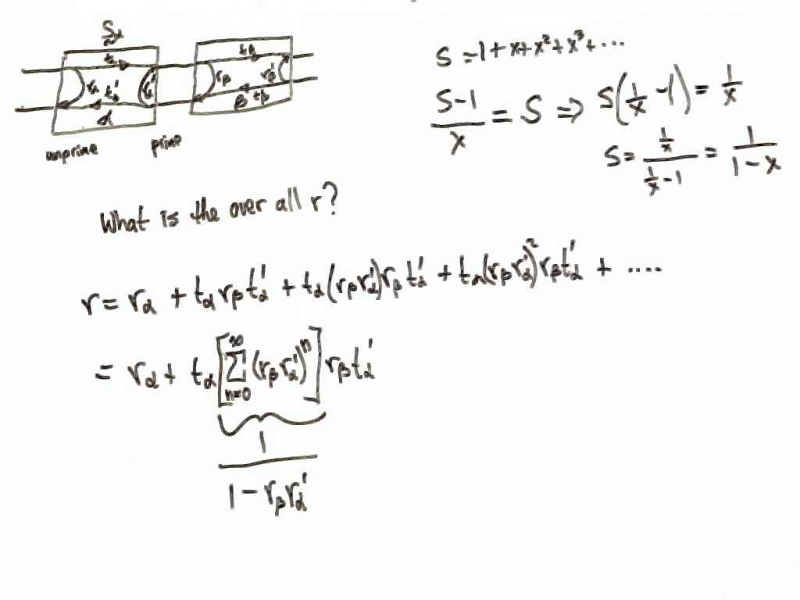For a more complete derivation see the Propagation and Radiation Class Notes of January 19 and 21, 2005. All the Feynman paths are summed using a geometric series to come up with the overall reflection coefficient. It should be noted that this works for n ports as well. All you do is define the sub matrices t, t', r and r' so that the proper number of ports are connected and so that the proper number of ports end up as input ports and output ports. It should also be noted that a convenient way to change the characteristic impedance of a port is to cascade the scattering matrix for a zero length change in characteristic impedance. An Octave file that cascades S parameters is given below:

%% -- S = cascadeS1S2(S1,S2)
%%
%% From:
%%   --S1--S2--
%% To:
%%      --S--
%%
%%   --S is the resulting composite scattering matrix, (2x2xm), where m allows
%%       these to be a function of frequency if you like.
%%   --S1 is the left scattering matrix, (2x2xm), where m allows
%%       these to be a function of frequency if you like.
%%   --S2 is the right scattering matrix, (2x2xm), where m allows
%%       these to be a function of frequency if you like.
%%   
%% This function calculates the composite scattering matrix, give the scattering
%% matrices of the cascaded networks.  It uses the Redheffer rules derived in Rob
%% Frohne's Class Notes for Propagation and Radiation, January 21, 2005.
%%
%% To start with we will only do 2x2 S matrices, because that is what we need
%% now, but the derivation is much more general.
%
%function S = cascadeS1S2(S1,S2)
%  for m =1:size(S1,3)
%    S(1,1,m) = S1(1,1,m)+S1(1,2,m)/(1-S2(1,1,m)*S1(2,2,m))*S2(1,1,m)*S1(2,1,m);
%    S(1,2,m) = S2(1,2,m)/(1-S1(2,2,m)*S2(1,1,m))*S1(1,2,m);
%    S(2,1,m) = S1(2,1,m)/(1-S2(1,1,m)*S1(2,2,m))*S2(2,1,m);
%    S(2,2,m) = S2(2,2,m)+S2(2,1,m)/(1-S1(2,2,m)*S2(1,1,m))*S1(2,2,m)*S2(1,2,m);
%  endfor
%end
%

The other application on this page is how you use this method to come up with the scattering matrix for an unknown network between the vector network analyzer you are using and the place you actually connect your device under test that you wish to have the reflection coefficient for. The basic idea is that there are three quantities needed to in this scattering matrix, r, r', and tt'. You can solve for these using three measurements of knows loads, usually the short, the open and the load (of the characteristic impedance, $Z_{0}$). Then knowing the unknown network between your measurement device and the device under test, you can back solve for the unknown reflection of the device under test.