Aliasing: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
mNo edit summary |
||
| Line 1: | Line 1: | ||
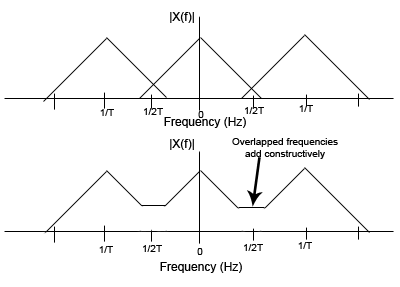
Alaising is what occurs when you sample the highest frequency component of a signal less than two times and then are not able to reconstruct the original signal from the sampled data. This is generalized by Nyquists sampling theorem that says the signal must be sampled at a frequency of 1/T > 2*fmax. | Alaising is what occurs when you sample the highest frequency component of a signal less than two times and then are not able to reconstruct the original signal from the sampled data. This is generalized by Nyquists sampling theorem that says the signal must be sampled at a frequency of 1/T > 2*fmax. In the example shown below a wave has a sample period of T and thus a sampling frequency of 1/T. fmax in this case is greater than 1/2T so there is some overlap in the bandwidth. This overlap of X(f) will add constructively in the sampled. Now when we wish to convert this sampled signal back to the the original we can not because we have no idea what it orginally looked like. | ||
[[Image:alias.gif]] | [[Image:alias.gif]] | ||
Revision as of 15:55, 10 December 2004
Alaising is what occurs when you sample the highest frequency component of a signal less than two times and then are not able to reconstruct the original signal from the sampled data. This is generalized by Nyquists sampling theorem that says the signal must be sampled at a frequency of 1/T > 2*fmax. In the example shown below a wave has a sample period of T and thus a sampling frequency of 1/T. fmax in this case is greater than 1/2T so there is some overlap in the bandwidth. This overlap of X(f) will add constructively in the sampled. Now when we wish to convert this sampled signal back to the the original we can not because we have no idea what it orginally looked like.