Alias: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
[[User:Harrde|Back to my page]] | [[User:Harrde|Back to my page]] | ||
==Aliasing== | |||
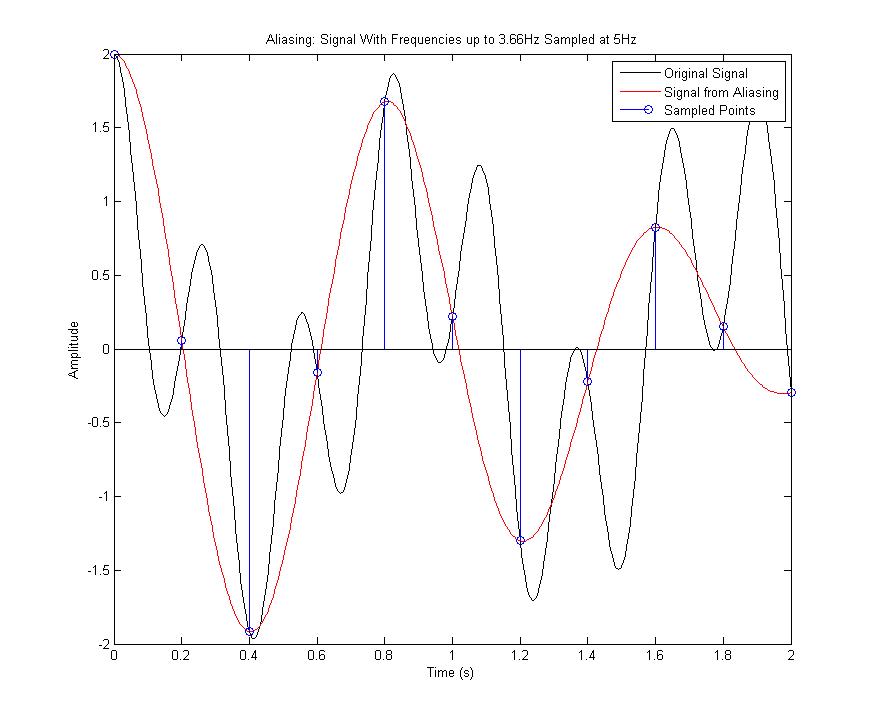
The Nyquist Theorem states that you must sample at a frequency which is twice that of the highest frequency components of the sampled signal in order to recover the sampled signal. If you sample at rate lower than this you get aliasing. Below is a figure which shows how aliasing occurs and the Matlab code for it. | |||
[[Image:harrdeH11Fig.jpg]] | [[Image:harrdeH11Fig.jpg]] | ||
<pre> | |||
clear all; | |||
Ts = .2; %Sampling time (s) | |||
ws = 2*pi/Ts; %Sampling frequency (rad/s) | |||
t = [0:0.005:2]; %Time vector | |||
w1 = 7; w2 = 23; | |||
y = cos(w1*t) + cos(w2*t); %Original Signal | |||
t1 = [0:Ts:2]; | |||
xs = cos(w1*t1) + cos(w2*t1); %Sampled points | |||
w2s = w2 - ws; | |||
x1 = cos(w1*t) + cos(w2s*t); %Signal from Aliasing | |||
figure(1); %Plot | |||
clf; | |||
plot(t,y,'k',t,x1,'r'); | |||
hold on | |||
stem(t1,xs); | |||
hold off; | |||
legend('Original Signal', 'Signal from Aliasing', 'Sampled Points'); | |||
xlabel('Time (s)'); | |||
ylabel('Amplitude'); | |||
title('Aliasing: Signal With Frequencies up to 3.66Hz Sampled at 5Hz'); | |||
</pre> | |||
Revision as of 12:54, 11 November 2007
Aliasing
The Nyquist Theorem states that you must sample at a frequency which is twice that of the highest frequency components of the sampled signal in order to recover the sampled signal. If you sample at rate lower than this you get aliasing. Below is a figure which shows how aliasing occurs and the Matlab code for it.
clear all;
Ts = .2; %Sampling time (s)
ws = 2*pi/Ts; %Sampling frequency (rad/s)
t = [0:0.005:2]; %Time vector
w1 = 7; w2 = 23;
y = cos(w1*t) + cos(w2*t); %Original Signal
t1 = [0:Ts:2];
xs = cos(w1*t1) + cos(w2*t1); %Sampled points
w2s = w2 - ws;
x1 = cos(w1*t) + cos(w2s*t); %Signal from Aliasing
figure(1); %Plot
clf;
plot(t,y,'k',t,x1,'r');
hold on
stem(t1,xs);
hold off;
legend('Original Signal', 'Signal from Aliasing', 'Sampled Points');
xlabel('Time (s)');
ylabel('Amplitude');
title('Aliasing: Signal With Frequencies up to 3.66Hz Sampled at 5Hz');