Samping by harrde: Difference between revisions
No edit summary |
|||
| Line 10: | Line 10: | ||
For a given input signal x(t) | For a given input signal x(t) | ||
[[Image:InputSignal.jpg]] | [[Image:InputSignal.jpg]] | ||
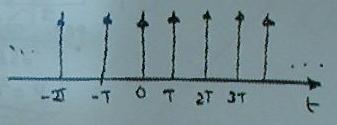
we want to sample this at time intervals T. This can be done by | :we want to sample this at time intervals T. This can be done by multiplying x(t) with a series of impulses | ||
[[Image:ImpulseString.jpg]] | [[Image:ImpulseString.jpg]] | ||
given by <math>\int_{-\infty}^\infty \delta(x) \, dx = 1.</math>. | :given by <math>\int_{-\infty}^\infty \delta(x) \, dx = 1.</math>. | ||
Revision as of 19:36, 12 November 2007
Sampling
Sampling is the process by which an anolog signal is converted into a digital signal and fed into digital circuit. Sampling is done by measuring the analog signal at a regular time interval. Each measurement of the anolog signal is called a sample. We can store and easily manupulate these samples in a computer and then interpolate between the sample points to fully reconstruct the original analog signal when we want to send the signal out of the computer. But we can only reconstruct orignal signal if we have sampled at a rate greater than twice the highest frequency component of the anolog signal. This restriction is given by the Nyquist Theorem which states:
Nyquist Theorem
A band-limited input signal can be recovered without distortion if it is sampled at a rate of at least twice the highest frequency component of interest within the signal.
How to Sample
- we want to sample this at time intervals T. This can be done by multiplying x(t) with a series of impulses
- given by .