Homework Eight

How does a CD player work with no oversampling, but digital filtering (1x oversampling)?

Nick Christman

---

Recall that when the audio for a music CD is produced it has an infinite amount of data points which can be expressed as $\scriptstyle x(t)$ in the time domain [Figure 1] and $\scriptstyle X(f)$ in the frequency domain [Figure 2].

Figure 1: Audio data as a function of time, x(t)

Figure 2: Audio data as a function of frequency, X(f)

When one wants to store the data of $\scriptstyle x(t)$ (i.e. reading the data onto a CD in this case) an infinite number of data points is not ideal -- in fact, it is impossible. Therefore, we must sample the data at the (typical) rate of $\scriptstyle f_{s}={\frac {1}{T}}$. This will give us a periodic function which we will call $\scriptstyle x(nT){\mbox{, where }}n\in \mathbb {Z} {\mbox{ and }}T$ is the sampling period. It is common to allow a sampling rate of twice the frequency at which a human can hear (i.e. 2 x 22 kHz) -- that means, $\scriptstyle f_{s}=44$ kHz.

Recall from class that in order to sample the original function, $\scriptstyle x(nT)$, we need to use a delta function. In other words, the continuous function of $\scriptstyle x(nT)$ can be written as $\sum _{n=-\infty }^{\infty }x(nT)\delta (t-nT_{0})$ [Figure 3]. As one may expect, in the frequency domain we should get the same plot as in Figure 2, but it should repeat. In the frequency domain, this can be expressed as ${\frac {1}{T}}\sum _{n=-\infty }^{\infty }X(f-{\frac {n}{T}})$ [Figure 4].

Figure 3: x(nT) written as impulses for sampling purposes

Figure 4: x(nT) written as impulses for sampling purposes in the frequency domain

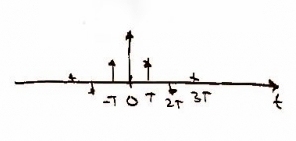
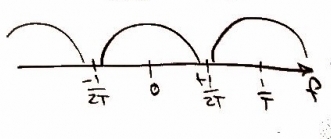
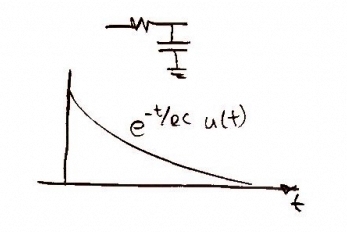
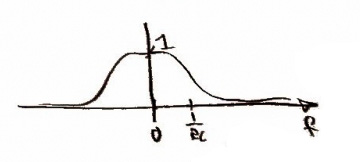
As one may suspect, in order to get a more accurate function you must take more data points -- in other words, a higher sampling rate (i.e. 2x, 8x, etc. oversampling) leads to a more accurate collection of data. For this case, we are asked to looked a digital sampling, or 1x oversampling. In order to accomplish this, we will convolve our function from above with a Finite Impulse Response filter (FIR filter). Let's call the FIR g(t) and define it as $\sum _{-M}^{M}g({\frac {mT}{p}})\delta (t-{\frac {mT}{p}})$ where $\scriptstyle p$ is the oversampling rate. In our case $\scriptstyle p=1$. Because we are dealing with digital sampling, the convolution will result in the original function [Figure 5]. It is fairly easy to see that in the frequency domain, the FIR filter will be expressed as $G(f)=\sum _{-M}^{M}g(mT)e^{-j2\pi mT}$ [Figure 6].

Figure 5: FIR filter in time domain, g(t)

Figure 6: FIR filter in frequency domain, G(f)

As we know, convolution in the time domain results in multiplication in the frequency domain. The results of the convolution and multiplication of the before mentioned FIR filter (time, frequency) are shown below:

Figure 7: Original function, x(nT), convolved with the FIR filter, g(t)

Figure 8: Original function multiplied by the FIR filter in frequency domain

At this point, we are ready to send the audio signal through a D/A converter -- which will essentially convolve the signal with a pulse function, say p(t). The pulse function is shown in the time domain [Figure 9] and the frequency domain [Figure 10]

Figure 9: Pulse function in the time domain, p(t)

Figure 10: Pulse function in the frequency domain, P(f)

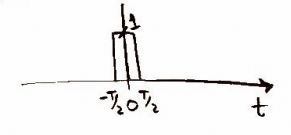
Note: P(f) is Tsinc(fT)

The convolution of the pulse function with the above FIR filtered function in the time domain [Figure 11] and the frequency domain [Figure 12] can be expressed as $\sum _{n=-\infty }^{\infty }x(nT)p(t-nT)$ and $P(f)\left[\sum _{n=-\infty }^{\infty }x(nT)e^{-j2\pi fnT}\right]$, respectively.

Figure 11: FIR filtered function convolved with p(t) (time)

Figure 12: FIR filtered function multiplied with P(f) (frequency)

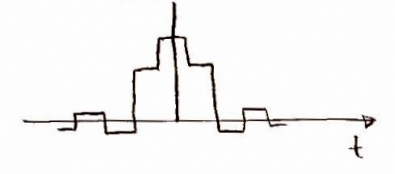
We are now very close to having the audio that we want -- now it would be good to run the signal through a low-pass filter to eliminate any high-frequency interference. As usual, we will convolve in time and multiply in frequency. The low pass filter in the time domain [Figure 13] and frequency domain [Figure 14] are shown below

Figure 13: Low pass filter in the time domain

Figure 14: Low pass filter in the frequency domain

This is how digital sampling would work -- our final signal should now be the audio we desire.