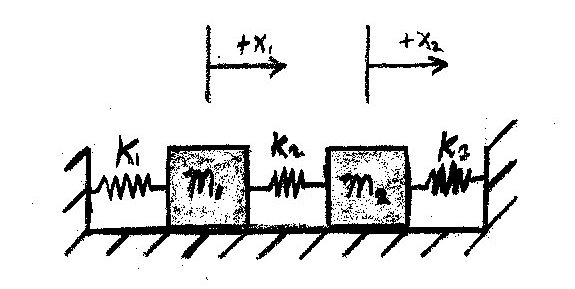
Coupled Oscillator: Hellie: Difference between revisions
Jump to navigation
Jump to search
| Line 15: | Line 15: | ||
:<math>k3=100 N/m\,</math> | :<math>k3=100 N/m\,</math> | ||
State Equations | |||
<math> | |||
\begin{bmatrix} | |||
\dot{x_1} \\ | |||
\ddot{x_1} \\ | |||
\dot{x_2} \\ | |||
\ddot{x_2} | |||
\end{bmatrix}\, | |||
</math> | |||
= | |||
<math> | |||
\begin{bmatrix} | |||
0&1&0&0 \\ | |||
0&0&0&0 \\ | |||
0&0&0&1 \\ | |||
0&0&0&0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
x_1 \\ | |||
\dot{x}_1 \\ | |||
x_2 \\ | |||
\dot{x}_2 | |||
\end{bmatrix} | |||
+ | |||
\begin{bmatrix} | |||
0&0&0&0 \\ | |||
0&0&0&0 \\ | |||
0&0&0&0 \\ | |||
0&0&0&0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
0\\ | |||
0\\ | |||
0\\ | |||
0 | |||
\end{bmatrix} | |||
</math> | |||
Eigenmodes | |||
Written by: Andrew Hellie | |||