HW10: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 26: | Line 26: | ||
sigC = real(ifft(sigA.*sigB));</pre> | sigC = real(ifft(sigA.*sigB));</pre> | ||
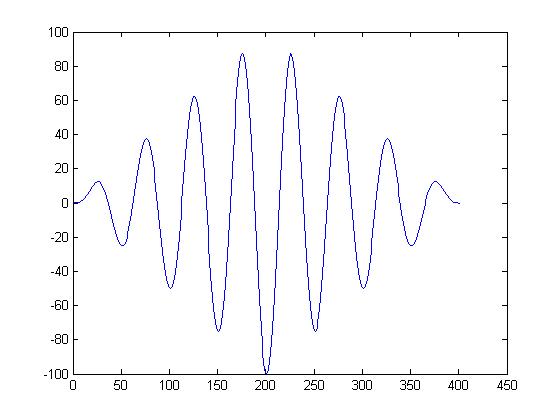
cross correlatoin of same wave<br> | |||
[[image:Same_wave.jpg]] | |||
cross correlation with 90degree delay<br> | |||
[[image:90degree_shift.jpg]] | |||
cross correlation with 45 degree delay<br> | |||
[[image:45shift.jpb | |||
cross correlation with <math>\frac{\pi}{1000}</math><br> | |||
[[image:Pi_onethousanths_shift.jpg]] | |||
Revision as of 22:22, 2 December 2009
Problem Statement
Present an Octave (or MATLAB) example using the discrete Fourier transform (DFT).
Solution
I decided to show a cross correlation example using MATLAB.
close all clear all f = 2; % sine wave frequency tmax = 2; % go to 2 seconds theta = pi/4; T = 0.01; t = 0:T:tmax; N = length(t); Nmat = 0:N-2; Zmat = Nmat *0; sig1 = sin(2*pi*f*t); % A alpha signal sig2 = sin(2*pi*f*t); % A beta signal c= conv(sig1,sig2); %test of matrix size %zeropad both vectors to length N1+N2-1 to avoid cyclic convolution sigA = fft([sig1 Zmat]); sigB = fft([sig2 Zmat]); sigC = real(ifft(sigA.*sigB));
cross correlatoin of same wave
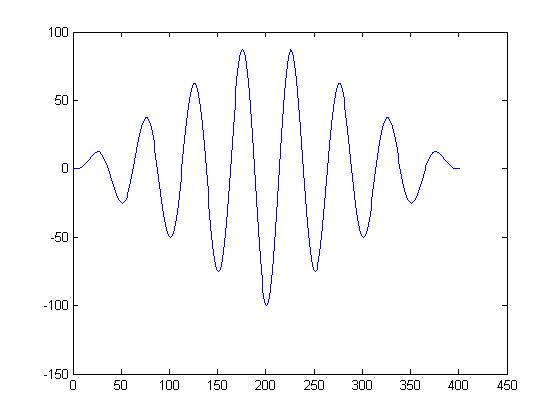
cross correlation with 90degree delay
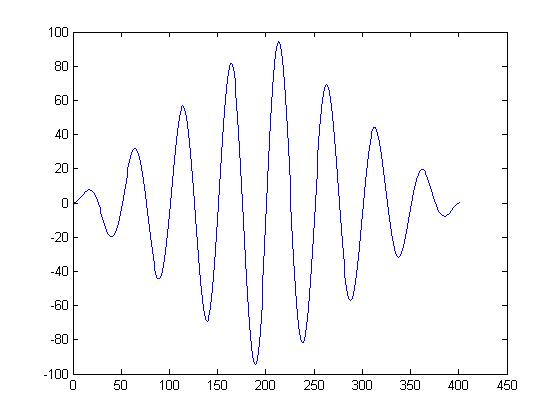
cross correlation with 45 degree delay
[[image:45shift.jpb