Coupled Oscillator: horizontal Mass-Spring: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
|||
| Line 5: | Line 5: | ||
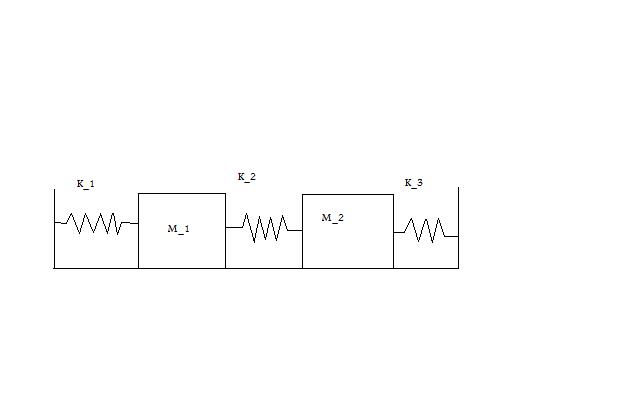
[[Image:horizontal spring.jpg]] | [[Image:horizontal spring.jpg]] | ||
'''Initial Conditions:''' | '''Initial Conditions:''' | ||
:<math>m_1= 10 kg\,</math> | |||
:<math>m_2 = 10 kg\,</math> | |||
:<math>k1=25 N/m\,</math> | |||
:<math>k2=75 N/m\,</math> | |||
:<math>k3=50 N/m\,</math> | |||
'''Equations for M_1''' | |||
:<math>\begin{alignat}{3} | |||
F & = ma \\ | |||
F & = m\ddot{x} \\ | |||
-k_{1}x_{1}-k_{2}(x_1x_2) & = m_1\ddot{x_1} \\ | |||
-{k_1x_1 \over {m_1}}-{k_2(x_1-x_2) \over {m_1}} & = m_1\ddot{x_1} \\ | |||
-{k_1x_1 \over {m_1}}-{k_2(x_1-x_2) \over {m_1}} & = \ddot{x_1} \\ | |||
-{k_1+k_2 \over {m_1}}x_1+{k_2 \over {m_1}}x_2 & = \ddot{x_1} \\ | |||
\end{alignat}</math> | |||
'''Equations for M_2''' | |||
:<math>\begin{alignat}{3} | |||
F & = ma \\ | |||
F & = m\ddot{x} \\ | |||
-k_2(x_2-x_1) & = m_2\ddot{x_2} \\ | |||
{-k_2(x_2-x_1) \over {m_2}} & = \ddot{x_2} \\ | |||
-{k_2 \over {m_2}}x_2+{k_2 \over {m_2}}x_1 & = \ddot{x_2} \\ | |||
\end{alignat}</math> | |||
'''Additional Equations''' | |||
:<math>\dot{x_1}=\dot{x_1}</math> | |||
:<math>\dot{x_2}=\dot{x_2}</math> | |||
'''State Equations''' | |||
<math> | |||
\begin{bmatrix} | |||
\dot{x_1} \\ | |||
\ddot{x_1} \\ | |||
\dot{x_2} \\ | |||
\ddot{x_2} | |||
\end{bmatrix}\, | |||
</math> | |||
= | |||
<math> | |||
\begin{bmatrix} | |||
0&1&0&0 \\ | |||
\frac{(k_1-k_2)}{m_1}&0&\frac{-k_1}{m_1}&0 \\ | |||
0&0&0&1 \\ | |||
\frac{k_1}{m_2}&0&\frac{(k_1+k_2)}{m_2}&0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
x_1 \\ | |||
\dot{x}_1 \\ | |||
x_2 \\ | |||
\dot{x}_2 | |||
\end{bmatrix} | |||
+ | |||
\begin{bmatrix} | |||
0&0&0&0 \\ | |||
0&0&0&0 \\ | |||
0&0&0&0 \\ | |||
0&0&0&0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
0\\ | |||
0\\ | |||
0\\ | |||
0 | |||
\end{bmatrix} | |||
</math> | |||
'''With the numbers...''' | |||
<math> | |||
\begin{bmatrix} | |||
\dot{x_1} \\ | |||
\ddot{x_1} \\ | |||
\dot{x_2} \\ | |||
\ddot{x_2} | |||
\end{bmatrix}\, | |||
</math> | |||
= | |||
<math> | |||
\begin{bmatrix} | |||
0&1&0&0 \\ | |||
\frac{(-50 N/m)}{15 kg}&0&\frac{-100 N/m}{15 kg}&0 \\ | |||
0&0&0&1 \\ | |||
\frac{100 N/m}{15 kg}&0&\frac{(250 N/m)}{15 kg}&0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
x_1 \\ | |||
\dot{x}_1 \\ | |||
x_2 \\ | |||
\dot{x}_2 | |||
\end{bmatrix} | |||
</math> | |||