Coupled Oscillator: horizontal Mass-Spring: Difference between revisions
Jump to navigation
Jump to search
| Line 129: | Line 129: | ||
= | = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
0 & | 0 & 0 & 0 & 0 \\ | ||
0 & 0 & 0 & 0 \\ | |||
0 & 0 & 0 & | 0 & 0 & 0 & 0 \\ | ||
0 & 0 & 0 & 0 | |||
\end{bmatrix} | \end{bmatrix} | ||
| Line 150: | Line 150: | ||
From this we get | From this we get | ||
:<math>\lambda_1= | :<math>\lambda_1=\,</math> | ||
:<math>\lambda_2= | :<math>\lambda_2=\,</math> | ||
:<math>\lambda_3= | :<math>\lambda_3=\,</math> | ||
:<math>\lambda_4= | :<math>\lambda_4=\,</math> | ||
Revision as of 13:53, 10 December 2009
Problem Statement
Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes and eigenvectors of the system.
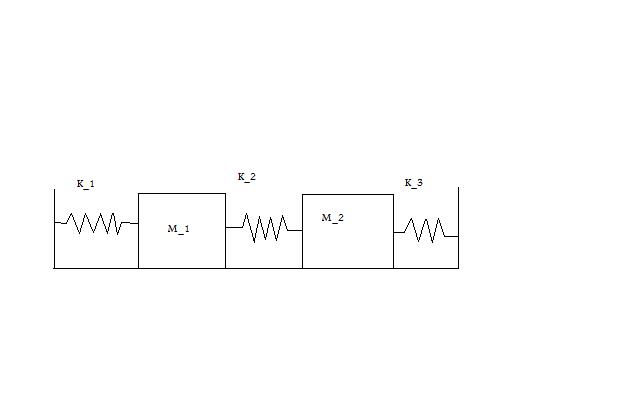
Initial Conditions:
Equations for M_1
Equations for M_2
Additional Equations
State Equations
=
With the numbers...
=
Eigen Values
Once you have your equations of equilibrium in matrix form you can plug them into a calculator or a computer program that will give you the eigen values automatically. This saves you a lot of hand work. Here's what you should come up with for this particular problem given these initial conditions.
- Given
We now have
From this we get