Fourier Example: Difference between revisions
Jump to navigation
Jump to search
Jorge.cruz (talk | contribs) |
Jorge.cruz (talk | contribs) |
||
| Line 40: | Line 40: | ||
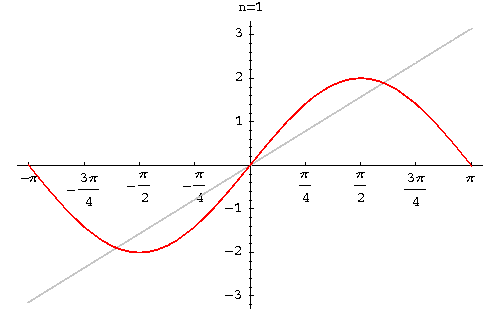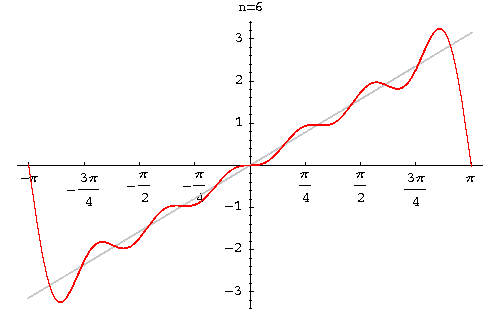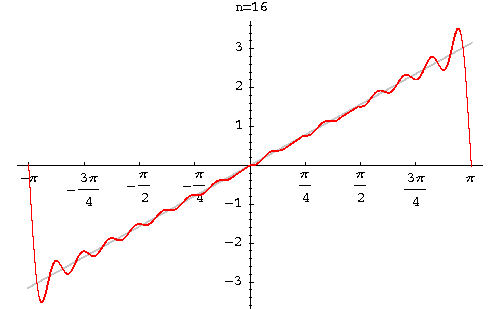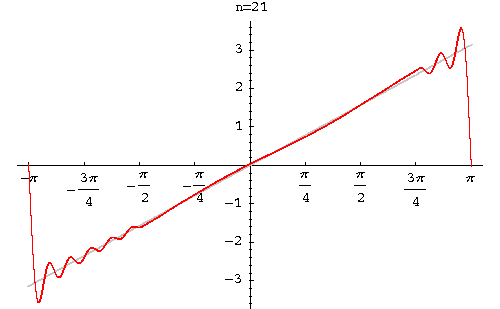
<math>f(x)=\frac{\pi}{2}+2(sin(x)+\frac{sin(3x)}{3}+\frac{sin(5x)}{5}+...)</math> | <math>f(x)=\frac{\pi}{2}+2(sin(x)+\frac{sin(3x)}{3}+\frac{sin(5x)}{5}+...)</math> | ||
[[Image:Fourier.gif]] | |||
==References:== | ==References:== | ||
[[Fourier Series: Basic Results]] | [[Fourier Series: Basic Results]] | ||
Revision as of 00:36, 19 January 2010
Find the Fourier Series of the function:
Solution
Here we have
and
We obtain = 0 and
Therefore, the Fourier series of f(x) is