Example: Metal Cart

Problem

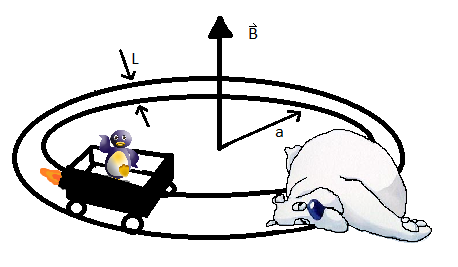
A DC generator is built using a metal cart with metallic wheels that travel around a set of perfectly conducting rails in a large circle. The rails are L m apart and there is a uniform magnetic ${\vec {B}}$ field normal to the plane as shown in Figure 1. The cart has a mass m and is driven by a rocket engine having a constant thrust $F_{1}$. A wet polar bear, having stumbled out of a shack where he recently had a bad experience with a battery, lays dead across the tracks acting as if a resistor R is connected as a load. Find The current as a function of time. What is the current after the generator attains the steady-state condition?

Solution

For this Problem we will represent the large circle as a pair of straight parallel wires and the cart as a single wire. This is illustrated below

FIGURE

We have two forces, $F_{1}$ being the force from the rocket engine and $F_{2}$ being the force caused by the current in the conductor and the Magnetic Field. The resulting Force $F_{t}$ is simply the sum of $F_{1}$ and $F_{2}$

$F_{2}$ can be found using Ampere's Law

${\vec {F}}=\int \limits _{c}I~{\vec {d}}l\times {\vec {B}}~~~~~\Longrightarrow ~~~~~{\vec {F}}_{2}=\int \limits _{0}^{L}I~{\vec {d}}l\times {\vec {B}}~~~~~\Longrightarrow ~~~~~{\vec {F}}_{2}=-I(t)~B~L~~{\hat {i}}$

We can also say that $I(t)={\frac {-e_{m}(t)}{R}}$

And $~~{e_{m}(t)}=\int \limits _{o}^{L}({\vec {v}}\times {\vec {B}})~{\vec {d}}l~~~~~\Longrightarrow ~~~~~{e_{m}(t)}=-v~L~B$

$I(t)={\frac {v~L~B}{R}}~~~~~~~~~~~~~~~~~~~~~~{\vec {F}}_{2}=-I(t)~B~L~~{\hat {i}}~~~~~\Longrightarrow ~~~~~{\vec {F}}_{2}=-{\frac {v~L~B}{R}}~B~L~~{\hat {i}}~~~~~\Longrightarrow ~~~~~{\vec {F}}_{2}=-{\frac {v~L^{2}~B^{2}}{R}}~~{\hat {i}}$

${\dot {v}}={\frac {F_{1}}{m}}~{\hat {i}}~+{\frac {F_{2}}{m}}~{\hat {i}}~~~~~\Longrightarrow ~~~~~{\dot {v}}=~{\frac {F_{1}}{m}}~~{\hat {i}}~-{\frac {v~L^{2}~B^{2}}{Rm}}~~{\hat {i}}~~~~~\Longrightarrow ~~~~~{\dot {v}}~+~v({\frac {L^{2}~B^{2}}{R~m}})~-~{\frac {F_{1}}{m}}~=~0$

Now we have a lovely differential equation to work with