Matthew's Asgn

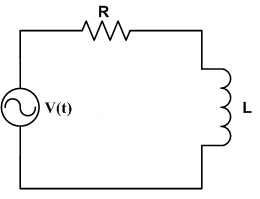
I decided that I would attempt to perform a simple analysis of a series RL circuit, which could then be used to do a more complex analysis on a basic transformer. I have always had interest in electronics, and transformers are key to basic electronics.

I decided that i would do the analysis of a RL circuit with the variables instead of given values.

Given:

V(t)=$\cos w*t$

V(s)=$s/(s^2+w^2)$

I(0)=i

The Laplace transform for an inductor:

${ℒ}\{f(t)\}$ = $Ls+Li$

The Laplace transform for a resistor:

${ℒ}\{f(t)\}$ = $R$

Therefore the Resulting Equation for the system after applying the Laplace Transform:

$0=\frac{-s}{(s^2+w^2)}+RI(s)+LsI(s)-Li$

A series of algebraic manipulations follows to come up with I(s):

$s/(s^2+w^2)=(R+Ls)I(s)+Li$

$I(s)=\frac{s}{(s^2+w^2)(R+Ls)}-\frac{Li}{(R+Ls)}$

We can then use partial fraction manipulation to expand the expression:

$\frac{s}{(s^2+w^2)(R+Ls)}=\frac{A}{(s+jw)}+\frac{A*}{(s-jw)}+\frac{B}{(Ls+R)}$

$(s/L)/((s^2+w^2)(R/L+s))=(A(s+jw)(s+R/L))/((s+R/L)(s^2+w^2))+(A*(s+jw)(s+R/L))/((s^2+w^2)(s+R/L))+(B(s^2+w^2))/((s+R/L)(s^2+w^2))$

$S/L=A((s-jw)(s+R/L))+A*((s+jw)(s+R/L))+B(s^2+w^2)=A(s^2-jws+R/Ls-jwR/L)+a*(s^2+jws+R/L+jwr/L)+B(s^2+w^2)$