HW10

Problem Statement

Present an Octave (or MATLAB) example using the discrete Fourier transform (DFT).

Solution

I decided to show a cross correlation example using MATLAB.

About cross correlation: First of all correlation is defined as
We may interpret the correlation operator as

which is $||x||^{2}=N$ times the coefficient of projection onto x of y advanced by n samples (shifted circularly to the left by n samples). The time shift n is called the correlation lag, and the function is called a lagged product.

This is then used to define cross correlation as

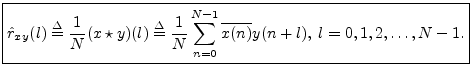
The term ``cross-correlation comes from statistics, and what is defined here is more properly called a ``sample cross-correlation.

This definition of a sample cross-correlation is only valid for stationary stochastic processes, e.g., ``steady noises that sound unchanged over time. The statistics of a stationary stochastic process are by definition time invariant, thereby allowing time-averages to be used for estimating statistics such as cross-correlations. For brevity below, we will typically not include ``sample qualifier, because all computational methods discussed will be sample-based methods intended for use on stationary data segments.

The DFT of the cross-correlation may be called the cross-spectral density, or ``cross-power spectrum, or even simply ``cross-spectrum:
File:Img15544.png

close all
clear all
f = 2; % sine wave frequency
tmax = 2; % go to 2 seconds
theta = pi/4;
T = 0.01; 
t = 0:T:tmax;
N = length(t);
Nmat = 0:N-2;
Zmat = Nmat *0;
sig1 = sin(2*pi*f*t); % A alpha signal
sig2 = sin(2*pi*f*t); % A beta signal
c= conv(sig1,sig2); %test of matrix size
%zeropad both vectors to length N1+N2-1 to avoid cyclic convolution
sigA = fft([sig1 Zmat]);
sigB = fft([sig2 Zmat]);
sigC = real(ifft(sigA.*sigB));

cross correlatoin of same wave

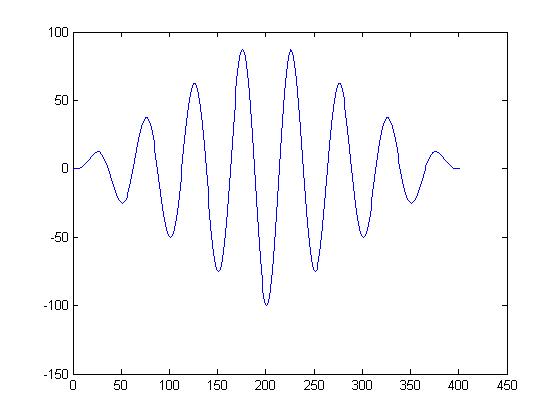
cross correlation with 90degree delay

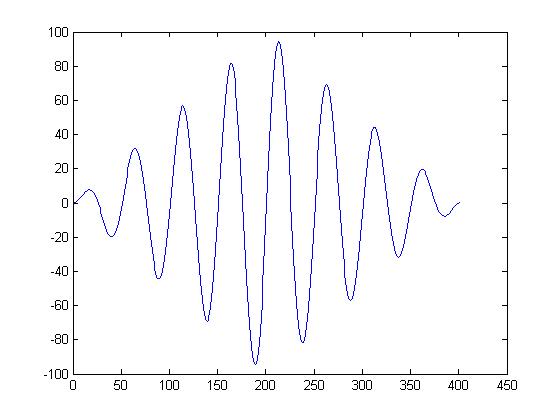
cross correlation with 45 degree delay
[[image:45shift.jpb

cross correlation with ${\frac {\pi }{1000}}$