Problem Statement
Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes of the system.
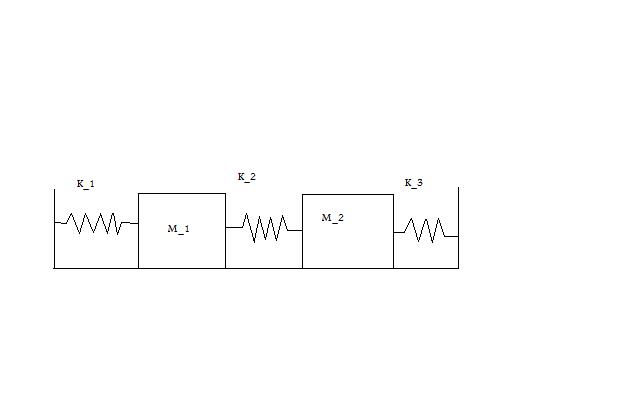
Initial Conditions:
Equations for M_1
Equations for M_2
Additional Equations
State Equations
=
With the numbers...
=