CD Player

A CD is a digitally recorded sound wave. The CD has a whole bunch of numbers on it. These numbers represent the magnitude of the sound wave at certain points in time. If your sound was a sine wave for example and you looked at it graphically you would see a smooth wave going up and down. A CD of this wave would just be the magnitude, or height, of that wave every so often. The basic idea in turning these numbers into a sound wave you can here is to run them through a digital to analog converter. The D-to-A will read in a value then output and hold a corresponding voltage until it gets the next value, then it will output and hold that voltage until the next one, etc. The end result will be a stair step representation of the original wave.

You can then run this through a low pass filter to smooth it out a little and then out to a speaker. While this would work your signal would be substantially distorted due to its conversion to and then from a digital signal. We will look at a few different ways to compensate for this.

Signal in Time and Frequency

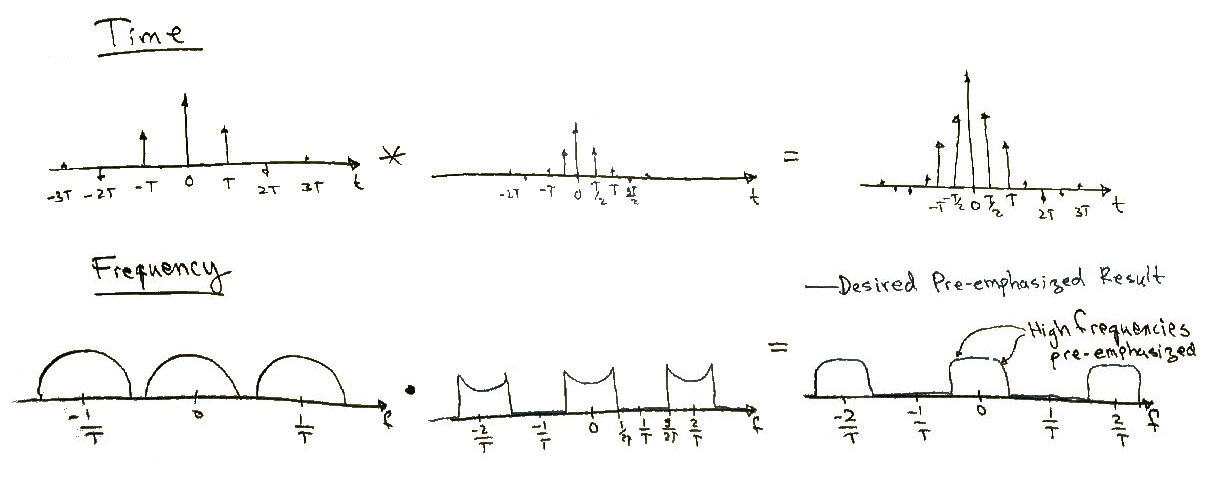
To get a better idea of why the signal becomes distorted and how to correct it, it helps to look at the signal in the time and the frequency domain. To represent the sampled signal in the time domain we will show a string of impulse functions whose area represents the magnitude of the signal at that point. While there is actually no impulse function physically in the system it is a useful mathematical construct to look at what is happening in the frequency domain.

File:Barnsasample.jpg

Figure 1

File:BarnsaDA.jpg

Figure 2

This shows the progression of your signal both in the time and frequency domains, as it is sampled (figure 1), and then ran through the D-to-A converter (figure 2). You will notice that the frequency representation of the stair step wave does not look like the original signal. It is too tall in the middle and drops off too fast of the edges; it also has too many high frequency (both positive and negative) components that aren't wanted. These high frequencies components need to be filtered off (which we stated above, the equivalent of smoothing out the stair step function in time) but you would still have to problem of the signal being too tall in the middle and dropping off too fast. In addition in order to filter out the high frequency parts and leave your signal unchanged you need a low pass filter with a very very sharp edge. This is a high precision and very spendy component that we would like to eliminate the need for. We have two basic problems, the distorted signal, and the need to filter out the high frequency components. To fix this we need to run the signal through some sort of filter that will both pre-distort the signal (increase its wanted high frequency components) and flatten out the unwanted high frequency components that are very close to the signal. This leads us into oversampling.

Over Sampling

The basic idea behind oversampling is to run the signal through an interpolation filter that will effectively double (or triple, or quadruple, etc) the number of points in the time signal. Suppose that there is a signal:

0 @ t=0

4 @ t=T

8 @ t=2T

The filter would guess at what the signal would be at 1/2T and 3/2T so the signal would become something like:

0 @ t=0

2 @ t=1/2T

4 @ t=T

6 @ t=3/2T

8 @ t=T

This is a very simple case, in actuality the filter would take a preset linear combination of the data points before and after to determine what the inserted value should be. Mathematically this is a convolution of the signal from the CD with a function of the form:

$f(t)=\sum _{l=-\infty }^{\infty }h({\frac {lT}{2}})\delta (t-{\frac {lT}{2}})$.

To see why this solves the problems stated above we need to look at the frequency domain. In the frequency domain we needed to filter out the unwanted higher frequencies to get our original signal back. To make this easier it would be nice to eliminate the frequencies that are really close to the signal you are trying to keep, and at the same time we wanted to pre-emphasize the high frequencies of our signal. This would mean multiplying them in frequency by a domain by a filtering function as shown below.

Multiplication in the frequency domain corresponds to a convolution in the time domain, and the function that we used above in the frequency domain corresponds to a string of impulses in time. Convolving by these impulses in time is the over sampling described above. This makes since because we have effectively doubled the frequency in the time domain which will space things out in the frequency domain and that is exactly what we see. The next logical question is, well that is nice but how do I actually do this on a computer. One way is with a Finite Impulse Response Filter of [FIR Filter].

Principle author of this page: Sam Barnes