FIR Filters

Finite Impulse Response Filters

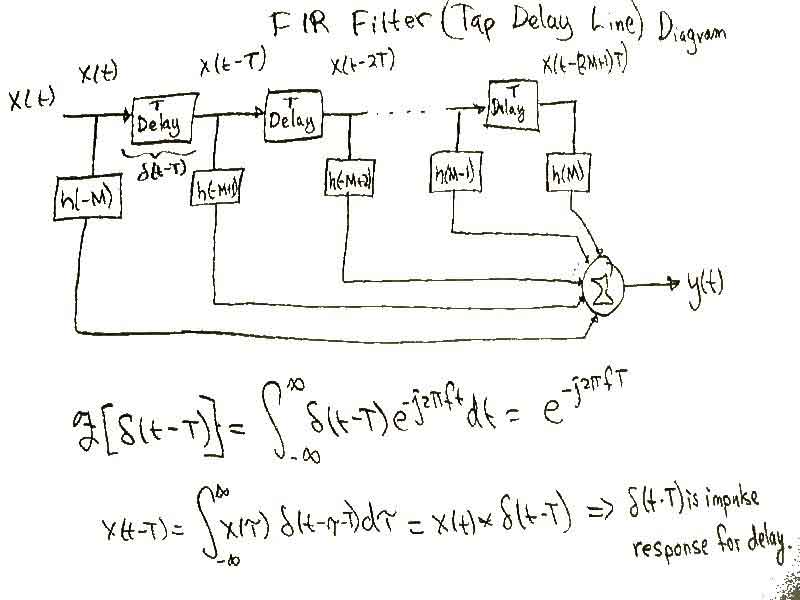
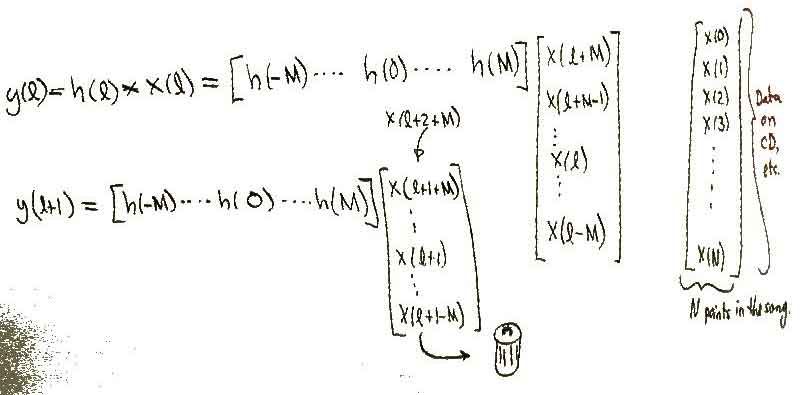
Above is shown the Tap Delay Line version of an FIR filter. It can actually be created in an analog circuit using transmission lines for the T Delay, resistors, an opamp, and an inverting summer to sum them all together. In the digital sense whats really happening here is that the output of the FIR filter (y(l)) is the convolution of h(l) with x(l) as shown below.

This filter can simply be viewed as a weighted average of the value around the time you are currently at, where h(l) would be the weighting coefficients. Mathematically it can be viewed as a multiply and accumulate because we are simply taking a predefined impulse function h() and multiplying it by x() then taking the next value of h() and multiplying it by the next value of x(). Then you just sum all those value together and that is the value of some y() at a certain time. Then you would move forward a step in time and throw out your oldest x() value and bring in the newest x() value to the top of your stack as shown in the picture.