Sampling - HW7
Max Woesner
Homework #7 - Sampling
Problem Statement
Figure out what happens if your sampled signal, , has frequency components only for . Can you recover the original signal from it? If so, find the expression for in terms of .
Solution
For frequency components , our sampled signal in the frequency domain, or , is going to look like this.

After sampling with frequency , the signal is going to be shifted over by , since . It will look like this.

To recover the original signal , we need to a use bandpass filter to filter out the parts we don't want, as indicated by the red line in the figure below. (Note: not to scale.)
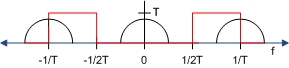
This leaves us with the original signal, as shown below.

The transfer function of the bandpass filter that will accomplish this for us is
To find the expression for , or the expression for the bandpass filter in the time domain, we can take the inverse Fourier transform of .
Recall , so
Also recall , so
Now that we know , we can find by convolving the function for after sampling with .
Or, if you prefer, <math> x(t) = \sum_{n=-\infty}^\infty x(nT)\Bigg[\frac{2sin\Big(\frac{2\pi (t-nT)}{T}\Big)}{\frac{2\pi (t-nT)}{T}} \ - \ \frac{sin\Big(\frac{\pi (t-nT)}{T}\Big)}{\frac{\pi (t-nT)}{T}}\Bigg]