8 - 1x oversampling

Write a section on the Wiki about how a CD player works with no oversampling, but digital filtering (1x oversampling)

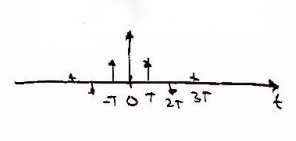
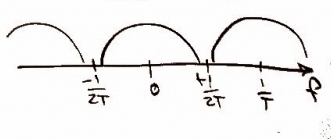
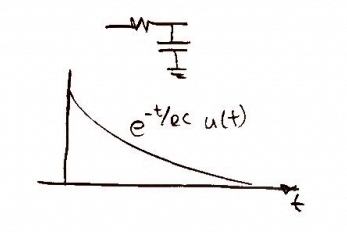
First we sample the data at $f_s=\frac{1}{T}$ to get the data in digital form and when you use the impulse function in time the frequency repeats forever as shown

                                 Sample $f_s=\frac{1}{T}⟹$

Where the impulse function with respect to time = $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(nt)\delta (t-nT)$
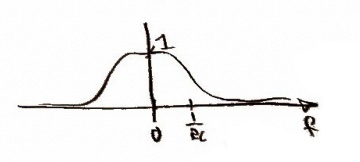
and $\frac{1}{T}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}X(f-\frac{n}{T})$ in the frequency domain.

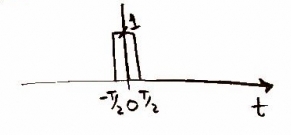
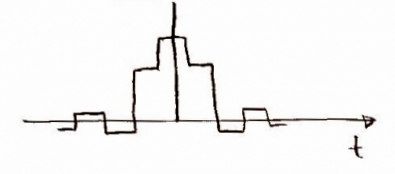
Now that we have the data in the computer we want to convolve it with another impulse function $\sum _{m=-M}^{M}h(\frac{mT}{n})\delta (t-\frac{mT}{n})$ in the time domain. This is where more that 1x oversampling would occur replace n for nx oversampling, but in our case we use n = 1. Doing this convolution we can also shape our frequency when you convolve in time it multiplies in frequency. So we pick a frequency function $\sum _{m=-M}^{M}h(\frac{mT}{n})e^{-j2\pi fm\frac{T}{n}}$ to multiply by so our frequency won't overlap later and help compensate for losses in the D/A converter.

>